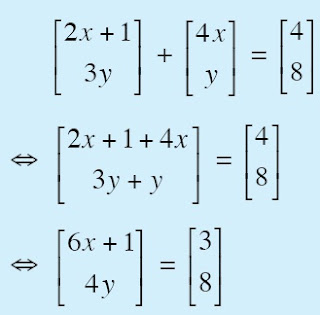Pintar Pelajaran Pola Soal Matriks, Pengertian, Jenis-Jenis, Sifat Operasi, Invers, Jawaban, Notasi Dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika

Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika - Apa yang kalian amati saat melihat daftar harga, daftar nilai UN, atau daftar gaji? Apakah kalian memerhatikan susunan penulisannya? Jika susunan tersebut dituliskan untuk per hari atau per bulan atau bahkan per tahun niscaya akan menjadi sangat panjang. Perhatikan juga posisi tempat duduk akseptor ujian. Apa yang kalian bayangkan perihal posisi berderet dari depan ke belakang dan dari kiri ke kanan? Kasus-kasus di atas sanggup disajikan dengan gampang memakai matriks.

Tujuan Pembelajaran :

Setelah mempelajari belahan ini, diharapkan kalian dapat

menjelaskan ciri suatu matriks;
menuliskan informasi dalam bentuk matriks;
melakukan operasi aljabar atas dua matriks;
menentukan determinan matriks persegi ordo 2;
menentukan invers matriks persegi ordo 2;
menentukan penyelesaian sistem persamaan linear dua variabel dengan invers matriks;
menentukan penyelesaian sistem persamaan linear dua variabel dengan determinan;
menentukan determinan matriks persegi ordo 3;
menentukan penyelesaian sistem persamaan linear tiga variabel.

Materi perihal matriks merupakan bahan gres bagi kalian.

Pembahasan perihal matriks ini sangat dibutuhkan untuk mempelajari bahan lain dalam matematika, antara lain determinan, vektor, dan transformasi geometri. Matriks merupakan salah satu cara untuk mempermudah penyelesaian sistem persamaan linear. Dalam kehidupan sehari-hari, matriks sangat membantu dalam mencatat hal-hal yang bekerjasama dengan jajaran bilangan.

1. Pengertian, Notasi, dan Ordo Matriks

1.1. Pengertian Matriks

Untuk memahami pengertian perihal matriks, perhatikan pola berikut. Seorang siswa mencatat hasil ulangan hariannya untuk pelajaran Matematika, Sejarah, TIK, dan Bahasa Inggris dalam tabel berikut.

Mata Pelajaran	Ulangan I	Ulangan II	Ulangan III	Ulangan IV
Matematika	7	8	9	8
Sejarah	8	7	8	6
TIK	5	7	8	6
B. Inggris	7	9	10	8

Tabel di atas sanggup disajikan dalam bentuk yang lebih sederhana.

Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika

Dalam membaca tabel di atas, siswa tidak mengalami kesulitan sebab beliau sudah tahu bahwa baris ke-1 ialah nilai Matematika, baris ke-2 nilai Sejarah, baris ke-3 nilai TIK, dan baris ke-4 nilai Bahasa Inggris. Untuk kolom pertama menyatakan nilai ulangan I, kolom ke-2 ialah nilai ulangan II, dan seterusnya.

Dalam matematika, susunan bilangan yang ditulis berdasarkan baris dan kolom serta ditandai dengan tanda kurung di sebelah kiri dan sebelah kanannya disebut matriks. Nama baris dan kolom diadaptasi dengan urutannya. Masing-masing bilangan yang ada di dalam tanda kurung tersebut disebut elemen matriks. Pada matriks di atas, elemen matriks baris ke-2 kolom ke-4 ialah 6 dan elemen matriks baris ke-3 kolom ke-1 ialah 5. Hal ini sanggup dilihat dengan gampang pada matriks berikut.

Pada matriks di atas, elemen matriks baris ke-3 kolom ke-4 ialah 6. Elemen matriks baris ke-2 kolom ke-3 ialah 8.

1.2. Notasi dan Ordo Matriks

Untuk menyatakan matriks, biasanya dipakai abjad kapital, menyerupai A, B, C, ..., sedangkan untuk menyatakan elemen matriks ditulis dengan abjad kecil. Misalnya, a_ij untuk menyatakan tiap elemen matriks A, b_ij untuk menyatakan tiap elemen B, dan seterusnya.

Dari uraian yang telah disampaikan di atas, kita sanggup mendefinisikan pengertian matriks sebagai berikut.

Suatu matriks A berukuran m × n ialah susunan berbentuk persegi panjang yang terdiri atas m baris dan n kolom.

Matriks A biasanya dinotasikan sebagai berikut.

a_ij menyatakan elemen matriks pada baris ke-i dan kolom ke-j.

Untuk ukuran m × n, sering kali disebut ordo suatu matriks sehingga matriks A sanggup ditulis A_{m x n}. Kadang-kadang, bentuk umum matriks A sanggup dituliskan secara singkat ke dalam notasi A = (a_ij), B = (b_ij), dan seterusnya.

Dari uraian di atas sanggup diberikan definisi yang terperinci perihal ordo matriks dan notasi matriks sebagai berikut.

Ordo suatu matriks ialah ukuran matriks yang menyatakan banyak baris diikuti dengan banyak kolom. Notasi dari matriks A dinyatakan dengan A = (a_ij).

Contoh Soal Matriks 1

Hasil penelitian perihal keadaan harga-harga pokok selama tahun 2004, 2005, 2006, dan 2007 di suatu kawasan ialah sebagai berikut.

Tahun	Harga Per Kilogram dalam Rupiah
Tahun	Beras	Gula	Minyak Goreng
2004	1.900	3.750	4.500
2005	2.300	3.900	4.700
2006	2.400	3.800	5.000
2007	2.600	4.000	5.600

a. Susunlah data di atas ke dalam bentuk matriks dengan notasi A.

b. Berapa banyak baris dan kolom dari matriks A?

c. Sebutkan elemen-elemen pada baris kedua.

d. Sebutkan elemen-elemen pada kolom ketiga.

Pembahasan Soal Matriks 1

a. A = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

b. Banyak baris pada matriks A ialah 4 dan banyak kolom pada matriks A ialah 3.

c. Elemen-elemen pada baris kedua adalah a₂₁ = 2.300, a₂₂ = 3.900, dan a₂₃ = 4.700.

d. Elemen-elemen pada kolom ketiga adalah a₁₃ = 4.500, a₂₃ = 4.700, a₃₃ = 5.000, dan a₄₃ = 5.600.

Contoh Soal 2

Diketahui matriks B = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

Tentukan :

a. ordo matriks B;

b. elemen-elemen baris pertama;

c. elemen pada baris ke-3 dan kolom ke-2;

d. elemen pada baris ke-2 dan kolom ke-4.

Penyelesaian 2

a. Matriks B mempunyai 3 baris dan 4 kolom sehingga ordo matriks B ialah 3 × 4 atau dinotasikan B_{3 × 4}.

b. Elemen-elemen baris pertama ialah 7, –5, 1, dan 8.

c. Elemen pada baris ke-3 kolom ke-2 ialah 3, ditulis b₃₂ = 3.

d. Elemen pada baris ke-2 kolom ke-4 ialah 9, ditulis b₂₄ = 9.

Contoh Soal 3

Diketahui sistem persamaan linear berikut.

3x + 5y – x = 4

5x + 2y – 3z = 8

2x – 4y + 2z = 6

a. Susunlah sistem persamaan linear di atas ke dalam matriks A.

b. Tentukan ordo matriks A.

c. Hitunglah a₃₂ + a₂₁ + a₁₃.

Jawaban 3

a. Sistem persamaan linear di atas sanggup disusun dalam tabel berikut.

	Koefisien x	Koefisien y	Koefisien z
Persamaan 1	3	5	–1
Persamaan 2	5	2	–3
Persamaan 3	2	–4	2

Dengan demikian, matriks yang bersesuaian dengan tabel di atas ialah A = $+\begin{bmatrix}+3+&+5&+-1+\\+5+&+2+&+-3+\\+2+&+-4&+2+\+\end{bmatrix}$

b. Ordo matriks A ialah 3 × 3 atau ditulis A_{3 × 3}.

c. a₃₂ adalah elemen baris ke-3 kolom ke-2, yaitu –4.

a₂₁ adalah elemen baris ke-2 kolom ke-1, yaitu 5.

a₁₃ adalah elemen baris ke-1 kolom ke-3, yaitu –1.

Jadi, a₃₂ + a₂₁ + a₁₃ = –4 + 5 + (–1) = 0.

1.3. Matriks-Matriks Khusus

Beberapa macam matriks khusus yang perlu kalian kenal ialah sebagai berikut.

1.3.1. Matriks Baris

Matriks baris ialah matriks yang hanya terdiri atas satu baris.

Misalnya:

P = [3 2 1]

Q = [4 5 –2 5]

1.3.2. Matriks Kolom

Matriks kolom ialah matriks yang hanya terdiri atas satu kolom, Misalnya:
$Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

1.3.3. Matriks Persegi

Matriks persegi ialah matriks yang banyak baris sama dengan banyak kolom. Jika banyak baris matriks persegi A ialah n maka banyaknya kolom juga n, sehingga ordo matriks A ialah n × n. Seringkali matriks A yang berordo n × n disebut dengan matriks persegi ordo n. Elemen-elemen a₁₁, a₂₂, a₃₃, ..., a_nn merupakan elemen-elemen pada diagonal utama.

Misalnya:

A = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$ merupakan matriks persegi ordo 2.

B = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$ merupakan matriks persegi ordo 4.

Elemen-elemen diagonal utama matriks A ialah 1 dan 10, sedangkan pada matriks B ialah 4, 6, 13, dan 2.

1.3.4. Matriks Diagonal

Matriks diagonal ialah matriks persegi dengan setiap elemen yang bukan elemen-elemen diagonal utamanya ialah 0 (nol), sedangkan elemen pada diagonal utamanya tidak semuanya nol. Misalnya:
$Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

1.3.5. Matriks Identitas

Matriks identitas ialah matriks persegi dengan semua elemen pada diagonal utama ialah 1 (satu) dan elemen lainnya semuanya 0 (nol). Pada umumnya matriks identitas dinotasikan dengan I dan disertai dengan ordonya. Misalnya:
$Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

1.3.6. Matriks Nol

Matriks nol ialah suatu matriks yang semua elemennya ialah 0 (nol). Matriks nol biasanya dinotasikan dengan abjad O diikuti ordonya, O_{m × n}. Misalnya:
$Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

1.4. Transpose Suatu Matriks

Transpose dari matriks A berordo m × n ialah matriks yang diperoleh dari matriks A dengan menukar elemen baris menjadi elemen kolom dan sebaliknya, sehingga berordo n × m. Notasi transpose matriks m n A × adalah $+A_{nxm}^{T}$ .

Contoh Soal 5 :

Jika A = $+\begin{bmatrix}+4+&2+&-1\\+3+&5+&6+\end{bmatrix}$ , tentukan A^T dan ordonya.

Pembahasan :

Terlihat dari matriks A bahwa elemen baris ke-1 ialah 4, 2, dan –1, sedangkan elemen baris ke-2 ialah 3, 5, dan 6. Untuk mengubah matriks A menjadi A^T, posisikan elemen baris ke-1 menjadi kolom ke-1 dan elemen baris ke-2 menjadi elemen kolom ke-2 sehingga diperoleh A^T = $+\begin{bmatrix}+4+&3+\\+2+&5+\\+-1&6\end{bmatrix}$

Ordo matriks A ialah 2 × 3, sedangkan ordo AT ialah 3 × 2.

2. Kesamaan Dua Matriks

Coba perhatikan bahwa :

4 = 4;

5 = 3 + 2;

9 = 3³

Perhatikan juga dengan matriks berikut.
$+\begin{bmatrix}+1+&+4\\+2+&+3+\end{bmatrix}=\begin{bmatrix}+1+&+4\\+2+&+3+\end{bmatrix}$

Matriks tersebut ialah dua matriks yang sama. Demikian juga dengan matriks berikut.

$+\begin{bmatrix}+1+&+3+1\\+2+&+3+\end{bmatrix}=\begin{bmatrix}+1+&+2^{2}\\+2+&+2+1+\end{bmatrix}$

Tampak bahwa elemen-elemen seletak dari kedua matriks mempunyai nilai yang sama. Sekarang, apakah matriks $+\begin{bmatrix}+1+&+3\\+2+&+4+\end{bmatrix}=\begin{bmatrix}+1+&+2\\+3+&+4+\end{bmatrix}$ merupakan dua matriks yang sama? Coba selidiki, apakah elemen-elemen seletak dari kedua matriks mempunyai nilai yang sama?

Jika kalian telah memahami masalah di atas, tentu kalian sanggup memahami definisi berikut.

Dua matriks A dan B dikatakan sama, ditulis A = B kalau matriks A dan B mempunyai ordo yang sama dan semua elemen yang seletak bernilai sama. Elemen yang seletak ialah elemen yang terletak pada baris dan kolom yang sama.

Contoh Soal 5

Diketahui A = $+\begin{bmatrix}+4+&+3\\+2+&+1+\end{bmatrix}$ , B = $+=\begin{bmatrix}+2^{2}+&+\sqrt{9}\\+\frac{1}{2}\sqrt{16}+&+1+\end{bmatrix}$ , C = $+\begin{bmatrix}+4+&+-3\\+-2+&+1+\end{bmatrix}$ , dan D = $+\begin{bmatrix}+3+&4+&5\\+2+&1+&6+\end{bmatrix}$ .

Apakah A = B? Apakah A = C? Apakah A = D?

Pembahasan 5

Dari keempat matriks tersebut, tampak bahwa matriks A = B sebab ordonya sama dan elemen-elemen yang seletak nilainya sama. Matriks A ≠ C sebab meskipun ordonya sama, tetapi elemen-elemen seletak ada yang nilainya tidak sama, sedangkan A ≠ D sebab ordonya tidak sama.

Contoh Soal 6

Tentukan nilai x, y, dan z jika $+\begin{bmatrix}+x+&+12\\+1+&+2-y+\end{bmatrix}$ = $+\begin{bmatrix}+2+&+3y\\+1+&+z+\end{bmatrix}$

Jawaban 6

Karena kedua matriks di atas sama dan elemen-elemen yang seletak bernilai sama, diperoleh x = 2, 12 = 3y atau y = 4, dan 2 – y = z atau z = –2. Jadi, x = 2, y = 4, dan z = –2.

3. Penjumlahan dan Pengurangan Matriks

3.1. Penjumlahan Matriks

Jumlah matriks A dan B, ditulis matriks A + B, ialah suatu matriks yang diperoleh dengan menjumlahkan elemen-elemen yang seletak dari matriks A dan B.

Misalnya:

Matriks $+\begin{bmatrix}+a+&+c\\+b+&+d+\end{bmatrix}$ dapat dijumlahkan dengan matriks $+\begin{bmatrix}+e+&+f\\+g+&+h+\end{bmatrix}$ .

Matriks $+\begin{bmatrix}+a+&b+&c\\+d+&e+&f+\end{bmatrix}$ dapat dijumlahkan dengan matriks $+\begin{bmatrix}+g+&h+&i\\+j+&k+&l+\end{bmatrix}$ .

dan seterusnya.

Secara umum, kalau matriks A = [a_ij] dan B = [b_ij] maka matriks A + B = [a_ij] + [b_ij] = [a_ij + b_ij].

Bagaimana kalau kedua matriks mempunyai ordo yang tidak sama?

Misalnya:

matriks $+\begin{bmatrix}+a+&+c\\+b+&+d+\end{bmatrix}$ dengan matriks $+\begin{bmatrix}+a+&b+&c\\+d+&e+&f+\end{bmatrix}$ . Dapatkah kedua matriks itu dijumlahkan?

Coba kalian diskusikan dengan teman-temanmu. Setelah melaksanakan diskusi perihal permasalahan di atas, tentu kalian sanggup menyimpulkan sebagai berikut.

Syarat semoga dua matriks atau lebih sanggup dijumlahkan ialah mempunyai ordo yang sama.

Contoh Soal 7

Diketahui A = $+\begin{bmatrix}+5+&+-2\\+3+&+1+\end{bmatrix}$ , B = $+\begin{bmatrix}+4+&+2\\+5+&+-6+\end{bmatrix}$ , dan C = $+\begin{bmatrix}+3+&1+&-2\\+2+&5+&-3+\end{bmatrix}$ Tentukan :

a. A + B;

b. A + C.

Penyelesaian 7

a. A + B = $+\begin{bmatrix}+5+&+-2\\+3+&+1+\end{bmatrix}+\begin{bmatrix}+4+&+2\\+5+&+-6+\end{bmatrix}=\begin{bmatrix}+5+4+&+-2+2\\+3+5+&+1\left+(-6+\right+)+\end{bmatrix}=\begin{bmatrix}+9+&+0\\+8+&+-5+\end{bmatrix}$

b. A + C = $+\begin{bmatrix}+5+&+-2\\+3+&+1+\end{bmatrix}+\begin{bmatrix}+3+&1+&-2\\+2+&5+&-3+\end{bmatrix}$ tidak sanggup dijumlahkan sebab ordonya tidak sama.

Contoh Soal 8

Carilah nilai x dan y yang memenuhi $+\begin{bmatrix}+2x\:++\:+1+\\+3y+\end{bmatrix}+\begin{bmatrix}+4y+\\+y+\end{bmatrix}=\begin{bmatrix}+4+\\+8+\end{bmatrix}$

Jawaban 8

Terlihat dari persamaan matriks ini, diperoleh 6x + 1 = 3

↔ x = 1/3 dan 4y = 8 ↔ y = 2. Jadi, diperoleh nilai x = 1/3 dan y = 2.

3.2. Pengurangan Matriks

3.2.1. Lawan Suatu Matriks

Sebelum kita membahas perihal pengurangan matriks, terlebih dahulu akan kita bicarakan mengenai lawan suatu matriks.

Lawan suatu matriks A ialah suatu matriks yang elemen-elemennya merupakan lawan dari elemen-elemen matriks A. Secara lebih jelas, dari suatu matriks A = [a_ij] sanggup ditentukan lawan matriks yang ditulis dengan –A sehingga –A = [–a_ij]. Misalnya sebagai berikut.

Jika A = $+\begin{bmatrix}+4+&+3\\+2+&+1+\end{bmatrix}$ , lawan matriks A ialah –A = $+\begin{bmatrix}+-4+&+-3\\+-2+&+-1+\end{bmatrix}$

Jika B = $+\begin{bmatrix}+-3+&+0\\+2+&+-1\\+-1&4+\end{bmatrix}$ , lawan matriks B ialah –B = $+\begin{bmatrix}+3+&+0\\+-2+&+1\\+1&-4+\end{bmatrix}$

3.2.2. Pengurangan terhadap Matriks

Pengurangan matriks A dan B, ditulis A – B, ialah suatu matriks yang diperoleh dengan mengurangkan elemen-elemen yang bersesuaian letak dari matriks A dan B. Atau, matriks A – B ialah matriks yang diperoleh dengan cara menjumlahkan matriks A dengan lawan dari matriks B, yaitu A – B = A + (–B) dengan –B ialah lawan matriks B. Seperti halnya dengan penjumlahan matriks, syarat semoga dua matriks atau lebih sanggup dikurangkan ialah mempunyai ordo yang sama. Secara umum, jika

A = [a_ij] dan B = [b_ij] maka A – B = [a_ij] – [b_ij] = [a_ij] – [b_ij]

Contoh Soal 9

Diketahui A = $+\begin{bmatrix}+5+&+3\\+2+&+6+\end{bmatrix}$ dan B = $+\begin{bmatrix}+2+&+-1\\+0+&+-3+\end{bmatrix}$ . Tentukan A – B.

Jawaban 9

Cara 1:

Karena –B = $+-\begin{bmatrix}+2+&+-1\\+0+&+-3+\end{bmatrix}=\begin{bmatrix}+-2+&+1\\+0+&+3+\end{bmatrix}$ maka

A – B = A + (–B) = $+\begin{bmatrix}+5+&+3\\+2+&+6+\end{bmatrix}+\begin{bmatrix}+-2+&+1\\+0+&+3+\end{bmatrix}=\begin{bmatrix}+5+\left+(-2+\right+)+&+3+1\\+2+0+&+6+3+\end{bmatrix}=\begin{bmatrix}+3+&+4\\+2+&+9+\end{bmatrix}$

Cara 2:

A – B = $+\begin{bmatrix}+5+&+3\\+2+&+6+\end{bmatrix}-\begin{bmatrix}+2+&+-1\\+0+&+-3+\end{bmatrix}=\begin{bmatrix}+5-2+&+3-\left+(-1+\right+)\\+2-0+&+6-\left+(-3+\right+)+\end{bmatrix}=\begin{bmatrix}+3+&+4\\+2+&+9+\end{bmatrix}$

Contoh Soal 10

Hitunglah X kalau diketahui $+\begin{bmatrix}+6+&+-5\\+4+&+3+\end{bmatrix}+\:+X\:+=\begin{bmatrix}+2+&+3\\+10+&+0+\end{bmatrix}$

Penyelesaian 10

X = $+\begin{bmatrix}+2+&+3\\+10+&+0+\end{bmatrix}-\begin{bmatrix}+6+&+-5\\+4+&+3+\end{bmatrix}=\begin{bmatrix}+-4+&+8\\+6+&+-3+\end{bmatrix}$

3.3. Sifat-Sifat Penjumlahan Matriks

Agar kalian sanggup menemukan sendiri sifat-sifat penjumlahan matriks, lakukan Aktivitas berikut.

Aktivitas :

Tujuan : Menemukan sifat-sifat penjumlahan matriks

Permasalahan : Sifat-sifat apakah yang berlaku pada penjumlahan matriks?

Kegiatan : Kerjakan soal-soal berikut di buku tugas.

1. Diketahui matriks A = $+\begin{bmatrix}+3+&+2\\+1+&+5+\end{bmatrix}$ , B = $+\begin{bmatrix}+4+&+2\\+-1+&+5+\end{bmatrix}$ , dan C = $+\begin{bmatrix}+6+&+-5\\+7+&+8+\end{bmatrix}$ . Tentukan hasil penjumlahan berikut, lalu tentukan sifat apa yang berlaku.

a. A + B c. (A + B) + C

b. B + A d. A + (B + C)

2. Untuk matriks A = $+\begin{bmatrix}+3+&+-1&5\\+2+&+-2&7+\end{bmatrix}$ dan O = $+\begin{bmatrix}+0+&+0&0\\+0+&+0&0+\end{bmatrix}$ , dengan ordo A ialah 2 × 3 dan ordo O ialah 2 × 3, apakah A + O = O + A? Apakah A + O = O + A berlaku untuk semua matriks yang sanggup dijumlahkan?

3. Diketahui matriks A = $+\begin{bmatrix}+-2+&+6&8\\+5+&+-7&-4+\end{bmatrix}$ . Tentukan A + (–A) dan (–A) + A. Matriks apakah yang kalian peroleh?

Kesimpulan : Berdasarkan acara di atas, sifat apa saja yang kalian peroleh?

Berdasarkan Aktivitas di atas sanggup ditemukan sifat-sifat penjumlahan dan pengurangan matriks sebagai berikut. Jika A, B, dan C matriks-matriks yang berordo sama maka pada penjumlahan matriks berlaku sifat-sifat berikut.

a. A + B = B + A (sifat komutatif)

b. (A + B) + C = A + (B + C) (sifat asosiatif)

c. Unsur identitas penjumlahan, yaitu matriks O sehingga A + O = O + A = A.

d. Invers penjumlahan A ialah –A sehingga A + (–A) = (–A) + A = O.

Perhatian :

Untuk pengurangan matriks tidak berlaku sifat komutatif, sifat asosiatif, dan tidak mempunyai unsur identitas.

4. Perkalian Suatu Skalar dengan Matriks

4.1. Pengertian Perkalian Suatu Skalar dengan Matriks

Misalkan A suatu matriks berordo m × n dan k suatu skalar bilangan real. Matriks B = kA sanggup diperoleh dengan cara mengalikan semua elemen A dengan bilangan k, ditulis :

Contoh Soal 11

Diketahui A = $+\begin{bmatrix}+5+&+1\\+-3+&+2+\end{bmatrix}$ dan B = $+\begin{bmatrix}+4+&+6\\+-2+&+8+\end{bmatrix}$ .

Tentukan :

a. 3A; b. 6B; c. –3A + 2B.

Jawaban 11

4.2. Sifat-Sifat Perkalian Bilangan Real (Skalar) dengan Matriks

Perkalian bilangan real (skalar) dengan suatu matriks sanggup dilakukan tanpa syarat tertentu. Artinya, semua matriks dengan ordo sembarang sanggup dikalikan dengan bilangan real (skalar). Misalkan A dan B matriks-matriks berordo m × n serta k₁ dan k₂ bilangan real (skalar), berlaku sifat-sifat berikut.

a. k₁(A + B) = k₁A + k₁B

b. (k₁ + k₂)A = k₁A + k₂A

c. k₁(k₂A) = (k₁k₂) A

Bukti :

Di buku ini, hanya akan dibuktikan sifat a. Misalkan k1 skalar, A dan B matriks berordo m × n.

Cara menunjukan sifat ini sanggup juga dilakukan sebagai berikut.

Misalkan matriks A = [a_ij] dan B = [b_ij], dengan i = 1, 2, ..., m

dan j = 1, 2, ..., n

k₁(A + B) = k₁([a_ij] + [b_ij])

= k₁([a_ij + b_ij])

= [k₁(a_ij + b_ij)]

= [k₁a_ij + k₁b_ij]

= [k₁a_ij] + [k₁b_ij]

= k₁[a_ij] + k₁[b_ij]

= k₁A + k₁B .............................................. (terbukti)

5. Perkalian Matriks

5.1. Pengertian Perkalian Matriks

Untuk memahami pengertian perkalian matriks, perhatikan ilustrasi berikut ini. Rina membeli bolpoin dan buku di dua tempat yang berbeda. Di toko I, ia membeli 3 bolpoin dan 2 buku, sedangkan di toko II, ia membeli 4 bolpoin dan 3 buku. Harga bolpoin dan buku di kedua toko tersebut sama, yaitu Rp2.500,00 dan Rp4.000,00 per buah. Berapa uang yang dikeluarkan Rina?

Tempat	Bolpoin	Buku
Toko I	3	2
Toko II	4	3

Barang	Harga
Bolpoin	Rp2.500,00
Buku	Rp4.000,00

Untuk menghitung jumlah uang yang dibayar oleh Rina sanggup pribadi kita hitung dengan cara mengalikan banyaknya barang dengan harga masing-masing sebagai berikut.

Toko I : (3 × Rp2.500,00) + (2 × Rp4.000,00) = Rp15.500,00

Toko II : (4 × Rp2.500,00) + (3 × Rp4.000,00) = Rp22.000,00

Di samping itu, pernyataan di atas sanggup disajikan dalam bentuk matriks sebagai berikut.

P = $+\begin{bmatrix}+3+&+2\\+4+&+3+\end{bmatrix}$ menyatakan banyak bolpoin dan buku yang dibeli Rina. Baris 1 menyatakan toko I dan baris 2 untuk toko II.

Q = $+\begin{bmatrix}+2.500\\+4.000+\end{bmatrix}$ menyatakan harga masing-masing bolpoin dan buku. Daftar jumlah uang yang dikeluarkan Rina sanggup dilihat pada tabel berikut.

Tempat	Harga Pembelian
Toko I	3 × Rp 2.500,00 + 2 × Rp 4.000,00 = Rp 15.500,00
Toko II	4 × Rp 2.500,00 + 3 × Rp 4.000,00 = Rp 22.000,00

Tabel pengeluaran di atas bersesuaian dengan perkalian matriks P × Q, yaitu :

P × Q = $+\begin{bmatrix}+3+&+2\\+4+&+3+\end{bmatrix}\begin{bmatrix}+2.500\\+4.000+\end{bmatrix}=\begin{bmatrix}+3\:+x\:+2.500+&+2\:+x\:+4.000\\+4\:+x\:+2.500+&+3\:+x\:+4.000+\end{bmatrix}=\begin{bmatrix}+15.500\\+22.000+\end{bmatrix}$

Dari uraian di atas, matriks P berordo 2 × 2 dan matriks Q berordo 2 × 1, sedangkan P × Q berordo 2 × 1 sehingga denah perkalian dan hasil kalinya mempunyai kekerabatan sebagai berikut.

Secara umum, perkalian matriks didefinisikan sebagai berikut.

Misalkan A matriks berordo m × p dan B matriks berordo p × n maka A × B ialah suatu matriks C = [c_ij] berordo m × n yang elemen-elemennya pada baris ke-i, yaitu kolom ke-j (c_ij) diperoleh dari penjumlahan hasil kali elemen-elemen yang bersesuaian pada baris ke-i matriks A dan kolom ke-j matriks B.

Contoh Soal 12

Diketahui matriks A = $+\begin{bmatrix}+2\\+-1+\end{bmatrix}$ , B = [-3 2], C = $+\begin{bmatrix}+2+&+3\\+1+&+4+\end{bmatrix}$ , dan D = $+\begin{bmatrix}+4+&+-5&-1\\+2+&+6&1+\end{bmatrix}$

Tentukan :

a. A × B; c. C × D;

b. B × C; d. A × C.

Jawaban 12

a. Hasil perkalian dari A × B.

b. Hasil perkalian dari B × C.

c. Hasil perkalian dari B × C.

d. A × C = $+\begin{bmatrix}+2+\\+-1+\end{bmatrix}=\begin{bmatrix}+2+&+3\\+-1+&+4+\end{bmatrix}$ tidak sanggup dikalikan sebab banyak kolom matriks A tidak sama dengan banyak baris matriks C.

5.2. Pengertian Dikalikan dari Kiri dan Dikalikan dari Kanan

Syarat dua matriks sanggup dikalikan ialah kalau banyak kolom matriks kiri sama dengan banyak baris matriks kanan. Jika perkalian A × B ada (dapat dikalikan) maka dikatakan bahwa :

a. matriks B dikali dari kiri oleh matriks A;

b. matriks A dikali dari kanan oleh matriks B.

Contoh Soal 13

Diketahui matriks A = $+\begin{bmatrix}+4+&+-2\\+1+&+3+\end{bmatrix}$ dan B = $+\begin{bmatrix}+2+&+3\\+4+&+-2+\end{bmatrix}$ .

Tentukan hasil perkalian

a. matriks A dikali dari kiri oleh matriks B;

b. matriks A dikali dari kanan oleh matriks B.

Pembahasan 14

a. Matriks A dikalikan dari kiri oleh matriks B, berarti :

B x A = $+\begin{bmatrix}+2+&+3\\+4+&+-2+\end{bmatrix}\begin{bmatrix}+4+&+-2\\+1+&+3+\end{bmatrix}=\begin{bmatrix}+11+&+5\\+14+&+-14+\end{bmatrix}$

b. Matriks A dikalikan dari kanan oleh matriks B, berarti :

A x B = $+\begin{bmatrix}+4+&+-2\\+1+&+3+\end{bmatrix}\begin{bmatrix}+2+&+3\\+4+&+-2+\end{bmatrix}=\begin{bmatrix}+0+&+16\\+14+&+-3+\end{bmatrix}$

Tampak dari hasil di atas bahwa A × B ≠ B × A, artinya perkalian matriks tidak bersifat komutatif.

5.3. Sifat-Sifat Perkalian Matriks

Misalkan matriks A, B, dan C sanggup dikalikan atau dijumlahkan. Untuk memahami sifat-sifat perkalian matriks, lakukan Aktivitas berikut.

Aktivitas

Tujuan : Menemukan sifat-sifat perkalian matriks.

Permasalahan : Sifat-sifat apakah yang berlaku pada perkalian matriks?

Kegiatan : Kerjakan (selidiki) soal berikut di buku tugas.

Diketahui matriks A = $+\begin{bmatrix}+1+&+2\\+-2+&+0+\end{bmatrix}$ , B = $+\begin{bmatrix}+-2+&+3\\+4+&+5+\end{bmatrix}$ , dan C = $+\begin{bmatrix}+2+&+-3\\+1+&+0+\end{bmatrix}$ , . Jika k = 2, tentukan hasil perhitungan berikut.

a. A × B dan B × A. Apakah A × B = B × A?

Apa kesimpulanmu?

b. (A × B) × C dan A × (B × C).

Apakah akhirnya sama? Apa kesimpulanmu?

c. A × (B + C), (C × B) + (A × C), dan (A × C) + (A × B).

Bagaimana kekerabatan ketiga operasi perkalian matriks tersebut?

d. A × I dan I × A dengan I matriks identitas.

Hubungan apa yang terbentuk?

e. A × O dan O × A dengan O matriks nol ordo 2 × 2.

Apakah A × O = O × A = O?

f. (kA) × B dan k(A × B). Apakah (kA) × B = k(A × B)?

Kesimpulan : Sifat-sifat apakah yang kalian temukan dari acara di atas?

Berdasarkan Aktivitas di atas ditentukan sifat-sifat perkalian matriks sebagai berikut.

Jika k bilangan real (skalar); A, B, dan C matriks yang sanggup dikalikan; serta B dan C sanggup dijumlahkan maka berlaku sifat-sifat perkalian matriks sebagai berikut.

a. Tidak komutatif, yaitu A × B = B × A.

b. Asosiatif, yaitu (A × B) × C = A × (B × C).

c. Distributif, yaitu:

1) distributif kiri: A × (B + C) = (A × B) + (A × C);

2) distributif kanan: (A + B) × C = (A × C) + (B × C).

d. Perkalian matriks-matriks persegi dengan matriks identitas I, yaitu A × I = I × A = A (ordo I sama dengan ordo matriks A).

e. Perkalian dengan matriks O, yaitu A × O = O × A = O.

f. Perkalian dengan skalar, yaitu (k A) × B = k(A × B).

Aktivitas

Tujuan : Menentukan hasil perkalian matriks dengan sumbangan software komputer.

Permasalahan : Bagaimana cara menentukan hasil perkalian matriks dengan memakai software komputer?

Kegiatan : Kita akan menentukan matriks invers dengan Microsoft Excel. Fungsi yang dipakai ialah MMULT. Misalnya,

$+\begin{bmatrix}+1+&+2\\+3+&+4+\end{bmatrix}\begin{bmatrix}+1+&+4\\+5+&+6+\end{bmatrix}$

Untuk itu lakukan langkah-langkah berikut.

1. Masukkan elemen-elemen matriks pada sel-sel Microsoft Excel.

2. Tentukan hasil kali matriks A dengan B. Caranya ialah sebagai berikut. Blok sel-sel yang akan ditempati elemen-elemen matriks hasil kali dari matriks A dan B. Ketik = MMULT(, lalu sorot sel-sel yang mengandung matriks A tadi. Kemudian, ketik koma (,) . Sorot sel-sel yang mengandung elemen-elemen matriks B diikuti dengan mengetik ).

Tekan CTRL + SHIFT + ENTER maka matriks hasil kali dari A dan B akan muncul.

Kesimpulan : Jika kalian melaksanakan langkah-langkah yang diinstruksikan dengan benar, kalian akan memperoleh hasil berikut.

5.4. Perpangkatan Matriks Persegi

Jika n ialah sebuah bilangan bundar positif dan A suatu matriks persegi, maka Aⁿ = A × A × A × ... × A (sebanyak n faktor) atau sanggup juga dituliskan Aⁿ = A × A^n–1 atau An = A^n–1 × A.

Contoh Soal 14 :

Diketahui matriks A = $+\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}$ . Tentukan

a. A²; b. A³; c. 2A⁴.

Jawaban :

a. A² = A × A = $+\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}=\begin{bmatrix}+3+&+-8\\+-4+&+11+\end{bmatrix}$

b. A³ = A × A² = $+\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}\begin{bmatrix}+3+&+-8\\+-4+&+11+\end{bmatrix}=\begin{bmatrix}+11+&+-30\\+-15+&+41+\end{bmatrix}$

Dengan cara lain, yaitu A³ = A² × A, diperoleh :

A³ = A² × A = $+\begin{bmatrix}+3+&+-8\\+-4+&+11+\end{bmatrix}\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}=\begin{bmatrix}+11+&+-30\\+-15+&+41+\end{bmatrix}$

Ternyata, A² × A = A × A² = A³.

c. 2A⁴ = 2A × A³ = $+2\begin{bmatrix}+1+&+-2\\+-1+&+3+\end{bmatrix}\begin{bmatrix}+11+&+-30\\+-15+&+41+\end{bmatrix}=2\begin{bmatrix}+41+&+-112\\+-56+&+153+\end{bmatrix}=\begin{bmatrix}+82+&+-224\\+-112+&+306+\end{bmatrix}$

6. Invers Suatu Matriks

Dua hal penting yang dibutuhkan dalam mencari invers matriks ialah transpose dan determinan suatu matriks. Pada subbab sebelumnya, kalian telah mempelajari transpose matriks. Sekarang, kita akan mempelajari determinan matriks.

6.1. Determinan Suatu Matriks

6.1.1. Determinan Matriks Ordo 2 × 2

Misalkan A = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ adalah matriks yang berordo 2 × 2 dengan elemen a dan d terletak pada diagonal utama pertama, sedangkan b dan c terletak pada diagonal kedua. Determinan matriks A dinotasikan ”det A” atau |A| ialah suatu bilangan yang diperoleh dengan mengurangi hasil kali elemen-elemen pada diagonal utama dengan hasil kali elemen-elemen diagonal kedua.

Dengan demikian, sanggup diperoleh rumus det A sebagai berikut.

det A = $+\begin{vmatrix}+a+&b+\\+c+&+d+\end{vmatrix}$ = ad – bc

Contoh Soal 15 :

Tentukan determinan matriks-matriks berikut.

a. A = $+\begin{bmatrix}+5+&+2\\+4+&+3+\end{bmatrix}$ b. B = $+\begin{bmatrix}+-4+&+-1\\+3+&+2+\end{bmatrix}$

Penyelesaian :

a. det A = $+\begin{bmatrix}+5+&+2\\+4+&+3+\end{bmatrix}$ = (5 × 3) – (2 × 4) = 7

b. det B = $+\begin{bmatrix}+-4+&+-1\\+3+&+2+\end{bmatrix}$ = ((–4) × 2) – (3 × (–1)) = – 5

6.1.2. Determinan Matriks Ordo 3 × 3 (Pengayaan)

Jika A = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$ adalah matriks persegi berordo 3 × 3, determinan A dinyatakan dengan det A = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

Ada 2 cara yang sanggup dipakai untuk menentukan determinan matriks berordo 3 × 3, yaitu hukum Sarrus dan metode minor-kofaktor.

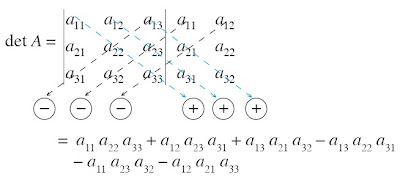
Aturan Sarrus

Untuk menentukan determinan dengan hukum Sarrus, perhatikan alur berikut. Misalnya, kita akan menghitung determinan matriks A_{3 × 3}. Gambaran perhitungannya ialah sebagai berikut.

Metode Minor-Kofaktor

Misalkan matriks A dituliskan dengan [a_ij]. Minor elemen aij yang dinotasikan dengan M_ij adalah determinan sehabis elemen-elemen baris ke-i dan kolom ke-j dihilangkan. Misalnya, dari matriks A_{3 × 3} kita hilangkan baris ke-2 kolom ke-1 sehingga :

Akan diperoleh M₂₁ = $+\begin{bmatrix}+a_{12}&a_{13}\\+a_{32}&a_{33}+\end{bmatrix}$ . M₂₁ adalah minor dari elemen matriks A baris ke-2 kolom ke-1 atau M₂₁ = minor a₂₁. Sejalan dengan itu, kita sanggup memperoleh minor yang lain, contohnya :

M₁₃ = $+\begin{bmatrix}+a_{21}&a_{12}\\+a_{31}&a_{32}+\end{bmatrix}$

Kofaktor elemen aij, dinotasikan K_ij adalah hasil kali (–1)^i+j dengan minor elemen tersebut. Dengan demikian, kofaktor suatu matriks dirumuskan dengan :

K_ij = (–1)^i+j M_ij

Dari matriks A di atas, kita peroleh contohnya kofaktor a₂₁ dan a₁₃berturut-turut adalah

K₂₁ = (–1)²⁺¹ M₂₁ = –M₂₁ = $+\begin{bmatrix}+a_{21}&a_{12}\\+a_{31}&a_{32}+\end{bmatrix}$

K₁₃ = (–1)¹⁺³ M₁₃ = M₁₃ = $+\begin{bmatrix}+a_{21}&a_{22}\\+a_{31}&a_{32}+\end{bmatrix}$

Kofaktor dari matriks A_{3 × 3} adalah kof(A) = $+\begin{bmatrix}+K_{11}+&+K_{12}&K_{13}\\+K_{21}+&+K_{22}&K_{23}\\+K_{31}+&+K_{32}&K_{33}+\end{bmatrix}$

Nilai dari suatu determinan merupakan hasil penjumlahan dari perkalian elemen-elemen suatu baris (atau kolom) dengan kofaktornya. Untuk menghitung determinan, kita sanggup menentukan dahulu sebuah baris (atau kolom) lalu kita gunakan hukum di atas. Perhatikan cara menentukan determinan berikut.

Misalkan diketahui matriks A = $Apa yang kalian amati saat melihat daftar harga Pintar Pelajaran Contoh Soal Matriks, Pengertian, Jenis-jenis, Sifat Operasi, Invers, Jawaban, Notasi dan Ordo, Penjumlahan, Pengurangan, Perkalian, Transpose, Skalar, Determinan, Matematika$

Determinan matriks A sanggup dihitung dengan cara berikut.

Kita pilih baris pertama sehingga

det A = a₁₁ K₁₁ + a₁₂ K₁₂ + a₁₃ K₁₃

= a₁₁ (–1)¹⁺¹ M₁₁ + a₁₂ (–1)¹⁺² M₁₂ + a₁₃ (–1)¹⁺³ M₁₃
₌ $+a_{11}\begin{bmatrix}+a_{22}+&+a_{23}\\+a_{32}+&+a_{33}+\end{bmatrix}-a_{12}\begin{bmatrix}+a_{21}+&+a_{23}\\+a_{31}+&+a_{33}+\end{bmatrix}+a_{13}\begin{bmatrix}+a_{21}+&+a_{22}\\+a_{31}+&+a_{32}+\end{bmatrix}$

= a₁₁(a₂₂ a₃₃ – a₃₂ a₂₃) – a₁₂(a₂₁ a₃₃ – a₃₁ a₂₃) + a₁₃(a₂₁ a₃₂ – a₃₁ a₂₂)

= a₁₁ a₂₂ a₃₃ – a₁₁ a₂₃ a₃₂ – a₁₂ a₂₁ a₃₃ + a₁₂ a₂₃ a₃₁ + a₁₃ a₂₁ a₃₂ – a₁₃ a₂₂ a₃₁

= a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a₃₁ + a₁₃ a₂₁ a₃₂ – a₁₃ a₂₂ a₃₁ – a₁₁ a₂₃ a₃₂ – a₁₂ a₂₁ a₃₃

Tampak bahwa det A matriks ordo 3 × 3 yang diselesaikan dengan cara minor kofaktor akhirnya sama dengan det A memakai cara Sarrus.

Contoh Soal 16

Tentukan determinan dari matriks A = $+\begin{vmatrix}+1+&2+&3+\\+2+&1+&4+\\+3&+1&+2+\end{vmatrix}$ dengan hukum Sarrus dan minor-kofaktor.

Penyelesaian 16

Cara 1: (Aturan Sarrus)

det A = $+\begin{vmatrix}+1+&2+&3+\\+2+&1+&4+\\+3&+1&+2+\end{vmatrix}$

= (1 × 1 × 2) + (2 × 4 × 3) + (3 × 2 × 1) – (3 × 1 × 3)

– (1 × 4 × 1) – (2 × 2 × 2)

= 2 + 24 + 6 – 9 – 4 – 8

= 11

Cara 2: (Minor-kofaktor)

Misalnya kita pilih perhitungan berdasarkan baris pertama sehingga diperoleh :

det A = $+1\begin{vmatrix}+1+&4+\\+1+&+2+\end{vmatrix}-2\begin{vmatrix}+2+&4+\\+3+&+2+\end{vmatrix}+3\begin{vmatrix}+2+&1+\\+3+&+1+\end{vmatrix}$

= –2 – 2(–8) + 3(–1)

= –2 + 16 – 3 = 11

Coba kalian selidiki nilai determinan ini dengan cara lain. Apakah akhirnya sama?

6.1.3. Sifat-Sifat Determinan Matriks

Berikut disajikan beberapa sifat determinan matriks

1. Jika semua elemen dari salah satu baris/kolom sama dengan nol maka determinan matriks itu nol.

Misal : $+A=\begin{bmatrix}+0+&+0\\+2+&+3+\end{bmatrix}\rightarrow+\left+|+A+\right+|=0;\:+B=\begin{bmatrix}+2+&+3+&+1\\+0+&+0+&+0\\+5+&+4+&+1+\end{bmatrix}\rightarrow+\left+|+B+\right+|=0$

2. Jika semua elemen dari salah satu baris/kolom sama dengan elemen-elemen baris/kolom lain maka determinan matriks itu nol.

Misal B = $+\begin{bmatrix}+4+&+3+&+2\\+5+&+7+&+8\\+4+&+3+&+2+\end{bmatrix}\rightarrow+\left+|+B+\right+|=0$ (Karena elemen-elemen baris ke-1 dan ke-3 sama).

3. Jika elemen-elemen salah satu baris/kolom merupakan kelipatan dari elemen-elemen baris/kolom lain maka determinan matriks itu nol.

Misal A = $+\begin{bmatrix}+1+&+2+&+3\\+5+&+7+&+0\\+2+&+4+&+6+\end{bmatrix}\rightarrow+\left+|+A+\right+|=0$ (Karena elemen-elemen baris ke-3 sama dengan kelipatan elemen-elemen baris ke-1).

4. |AB| = |A| ×|B|

5. |AT| = |A|, untuk AT ialah transpose dari matriks A.

6. |A^–1| = $+\frac{1}{\left+|+A+\right+|}$ , untuk A^–1 adalah invers dari matriks A. (Materi invers akan kalian pelajari pada subbab berikutnya).

7. |kA| = kn |A|, untuk A ordo n × n dan k suatu konstanta. Sifat-sifat di atas tidak dibuktikan di sini. Pembuktian sifat-sifat ini akan kalian pelajari di jenjang yang lebih tinggi.

6.2. Pengertian Invers Matriks

Misalkan dua matriks A dan B ialah matriks berordo n × n dan In ialah matriks identitas berordo n × n. Jika A × B = B × A = I_nmaka matriks A disebut invers matriks B, sebaliknya B disebut invers matriks A. Dalam keadaan menyerupai ini maka dikatakan bahwa A dan B saling invers.

Jika matriks A mempunyai invers, dikatakan bahwa matriks A ialah matriks nonsingular, sedangkan kalau A tidak mempunyai invers, matriks A disebut matriks singular. Invers matriks A ditulis A^–1.

Contoh Soal 17

Diketahui A = $+\begin{bmatrix}+2+&+1\\+3+&+2+\end{bmatrix}$ dan B = $+\begin{bmatrix}+2+&+-1\\+-3+&+2+\end{bmatrix}$

Selidiki, apakah A dan B saling invers?

Penyelesaian 17

Matriks A dan B saling invers kalau berlaku A × B = B × A = I.

A × B = $+\begin{bmatrix}+2+&+1\\+3+&+2+\end{bmatrix}\begin{bmatrix}+2+&+-1\\+-3+&+2+\end{bmatrix}=\begin{bmatrix}+1+&+0\\+0+&+1+\end{bmatrix}=I$

B × A = $+\begin{bmatrix}+2+&+-1\\+-3+&+2+\end{bmatrix}\begin{bmatrix}+2+&+1\\+3+&+2+\end{bmatrix}=\begin{bmatrix}+1+&+0\\+0+&+1+\end{bmatrix}=I$

Karena A × B = B × A maka A dan B saling invers, dengan A^–1 = B dan B^–1 = A.

6.3. Menentukan Invers Matriks Berordo 2 × 2

Misalkan diketahui matriks A = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ , dengan ad – bc ≠ 0.

Suatu matriks lain, contohnya B dikatakan sebagai invers matriks A kalau AB = I. Matriks invers dari A ditulis A^–1 . Dengan demikian, berlaku :

AA^–1 = A^–1A = I

Matriks A mempunyai invers kalau A ialah matriks nonsingular, yaitu det A ≠ 0. Sebaliknya, kalau A matriks singular (det A = 0) maka matriks ini tidak mempunyai invers.

Misalkan matriks A = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ dan matriks B = $+\begin{bmatrix}+p+&+q\\+r+&+s+\end{bmatrix}$ sehingga berlaku A × B = B × A = I. Kita akan mencari elemen-elemen matriks B, yaitu p, q, r, dan s.

Dari persamaan A × B = I, diperoleh :

$+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}\begin{bmatrix}+p+&+q\\+r+&+s+\end{bmatrix}=\begin{bmatrix}+1+&+0\\+0+&+1+\end{bmatrix}$
$+\begin{bmatrix}+ap+br+&+aq+bs\\+cp+dr+&+cq+ds+\end{bmatrix}=\begin{bmatrix}+1+&+0\\+0+&+1+\end{bmatrix}$

Jadi, diperoleh sistem persamaan :

ap + br = 1 dan aq + bs = 0

cp + dr = 0 cq + ds = 1

Dengan menuntaskan sistem persamaan tersebut, kalian peroleh :

$+p=\frac{d}{ad-bc},\:+r=\frac{-c}{ad-bc},\:+q=\frac{-b}{ad-bc},\:+dan\:+s=\frac{a}{ad-bc}$

Dengan demikian,

Matriks B memenuhi A × B = I.

Sekarang, akan kita buktikan apakah matriks B × A = I?

Karena ad – bc ≠ 0, berlaku B × A = $+\begin{bmatrix}+1+&+0\\+0+&+1+\end{bmatrix}$ = I

Karena A × B = B × A = I maka B = A^–1.

Jadi, kalau A = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ maka inversnya ialah :

$+A^{-1}=\frac{1}{ad-bc}\begin{bmatrix}+d+&+-b\\+-c+&+a+\end{bmatrix}$

untuk ad – bc ≠ 0.

Contoh Soal 18

Tentukan invers matriks-matriks berikut.

a. A = $+\begin{bmatrix}+4+&+1\\+7+&+2+\end{bmatrix}$

b. B = $+\begin{bmatrix}+3+&+-2\\+5+&+-4+\end{bmatrix}$

Jawaban 18

Aktivitas :

Tujuan : Menentukan invers matriks persegi dengan sumbangan software komputer.

Permasalahan : Bagaimana cara menentukan inver matriks dengan memakai software komputer?

Kegiatan : Kita akan menentukan matriks invers dengan Microsoft Excel. Fungsi yang dipakai ialah MINVERSE. Misalnya, akan ditentukan invers matriks $+\begin{bmatrix}+1+&+2\\+3+&+4+\end{bmatrix}$ . Untuk itu lakukan langkah-langkah berikut.

1. Masukkan elemen-elemen matriks pada sel-sel Microsoft Excel yang membentuk persegi.

2. Tentukan invers matriks A dengan cara berikut. Blok empat sel yang akan ditempati elemen-elemen matriks invers dari A. Ketik “=MINVERSE(”, lalu sorot sel-sel yang mengandung matriks A tadi. Diikuti dengan mengetik “)”.

Tekan CTRL + SHIFT + ENTER maka matriks invers dari A akan muncul.

Kesimpulan : Jika kalian melaksanakan langkah-langkah yang diinstruksikan dengan benar, kalian akan memperoleh hasil berikut.

6.4. Menentukan Invers Matriks Berordo 3 × 3 (Pengayaan)

Invers matriks berordo 3 × 3 sanggup dicari dengan beberapa cara. Pada pembahasan kali ini kita akan memakai cara adjoin dan transformasi baris elementer.

6.4.1. Dengan Adjoin

Pada subbab sebelumnya, telah dijelaskan mengenai determinan matriks. Selanjutnya, adjoin A dinotasikan adj (A), yaitu transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen-elemen matriks A, yaitu :

adj(A) = (kof(A))^T

Adjoin A dirumuskan sebagai berikut.

Invers matriks persegi berordo 3 × 3 dirumuskan sebagai berikut.

$+A^{-1}=\frac{1}{det\:+A}adj\left+(+A+\right+)$

Adapun bukti perihal rumus ini akan kalian pelajari lebih mendalam dijenjang pendidikan yang lebih tinggi.

Contoh Soal 19 :

Diketahui matriks A = $+\begin{bmatrix}+1+&+2&1\\+2+&+3&4\\+1+&+2&3+\end{bmatrix}$ . Tentukan invers matriks A, contohnya kita gunakan perhitungan berdasarkan baris pertama.

Jawaban :

Terlebih dahulu kita hitung determinan A.

det A = $+det\:+A=1\begin{vmatrix}+3+&+4\\+2+&+3+\end{vmatrix}-2\begin{vmatrix}+2+&+4\\+1+&+3+\end{vmatrix}+1\begin{vmatrix}+2+&+3\\+1+&+2+\end{vmatrix}$

= 1(1) – 2(2) + 1(1) = –2

Dengan memakai rumus adjoin A, diperoleh :

adj(A) = $+\begin{bmatrix}+1+&+-4&+5\\+-2+&+2&+-2\\+1+&+0&+-1+\end{bmatrix}$

Jadi, A^–1 dapat dihitung sebagai berikut.

6.4.2. Dengan Transformasi Baris Elementer

Untuk menentukan invers matriks An dengan cara transformasi baris elementer, sanggup dilakukan dengan langkah-langkah berikut berikut.

1) Bentuklah matriks (A_n | I_n), dengan In ialah matriks identitas ordo n.

2) Transformasikan matriks (A_n | I_n) ke bentuk (I_n | B_n), dengan transformasi elemen baris.

3) Hasil dari Langkah 2, diperoleh invers matriks A_n adalah B_n.

Notasi yang sering dipakai dalam transformasi baris elementer ialah :

a) B_i ↔ B_j : menukar elemen-elemen baris ke-i dengan elemen-elemen baris ke-j;

b) k.B_i : mengalikan elemen-elemen baris ke-i dengan skalar k;

c) B_i + kB_j : jumlahkan elemen-elemen baris ke-i dengan k kali elemen-elemen baris ke-j.

Contoh Soal 20

Tentukan invers matriks A = $+\begin{bmatrix}+2+&+1\\+5+&+3+\end{bmatrix}$ dengan transformasi baris elementer.

Penyelesaian :

Jadi, diperoleh A^–1 = $+\begin{bmatrix}+3+&+-1\\+-5+&+2+\end{bmatrix}$

Keterangan :

1/2 B₁ : Kalikan elemen-elemen baris ke-1 dengan 1/2.

B₂ – 5B₁ : Kurangkan baris ke-2 dengan 5 kali elemen-elemen baris ke-1.

B₁ – B₂ : Kurangi elemen-elemen baris ke-1 dengan elemen-elemen baris ke-2.

2B₂ : Kalikan elemen-elemen baris ke-2 dengan 2.

Contoh Soal 21 :

Tentukan invers matriks A = $+\begin{bmatrix}+1+&+1&+0\\+2+&+3&+2\\+2+&+1&+3+\end{bmatrix}$ dengan transformasi baris elementer.

Jawaban 20

6.5. Persamaan Matriks Bentuk AX = B dan XA = B

Misalkan A, B, dan X ialah matriks-matriks berordo 2 × 2, dengan matriks A dan B sudah diketahui elemennya, sedangkan matriks X belum diketahui elemen-elemennya. Matriks X sanggup ditentukan kalau A mempunyai invers (matriks nonsingular). Untuk menuntaskan persamaan matriks berbentuk AX = B sanggup dilakukan dengan langkah berikut.

AX = B

↔ A^–1(AX) = A^–1B

↔ (A^–1A)X = A^–1B

↔ IX = A^–1B

↔ X = A^–1B

Dari persamaan terakhir tampak bahwa kedua ruas dikalikan dari kiri oleh A^–1 sehingga diperoleh bentuk penyelesaian X = A^–1B. Untuk menuntaskan persamaan matriks berbentuk XA = B sanggup ditentukan dengan cara mengalikan kedua ruas dari kanan dengan A^–1 sehingga diperoleh penyelesaian X = BA^–1 seperti berikut.

XA = B

↔ (XA)A^–1 = BA^–1

↔ X(AA^–1) = BA^–1

↔ XI = BA^–1

↔ X = BA^–1

Oleh sebab itu, diperoleh penyelesaian X = BA^–1. Dengan demikian, sanggup disimpulkan sebagai berikut.

Penyelesaian persamaan matriks AX = B ialah X = A^–1B.

Penyelesaian persamaan matriks XA = B ialah X = BA^–1.

Untuk lebih jelasnya, perhatikan pola berikut.

Contoh Soal 22

Diketahui A = $+\begin{bmatrix}+8+&+3\\+5+&+2+\end{bmatrix}$ dan B = $+\begin{bmatrix}+2+&+-1\\+0+&+1+\end{bmatrix}$ .

Tentukan matriks X yang memenuhi

a. AX = B;

b. XA = B.

Jawaban 22

Karena det A = 16 – 15 = 1 ↔ 0 maka matriks A mempunyai invers.

Jika dicari inversnya, kalian akan memperoleh A^–1 = $+\begin{bmatrix}+8+&+3\\+5+&+2+\end{bmatrix}$

(Coba kalian tunjukkan).

Dengan demikian, sanggup kita tentukan sebagai berikut.

a. AX = B ↔ X = A^–1B = $+\begin{bmatrix}+2+&+-3\\+-5+&+8+\end{bmatrix}\begin{bmatrix}+2+&+-1\\+0+&+1+\end{bmatrix}=\begin{bmatrix}+4+&+-5\\+-10+&+13+\end{bmatrix}$

b. XA = B ↔ X = BA^–1 = $+\begin{bmatrix}+2+&+-1\\+0+&+1+\end{bmatrix}\begin{bmatrix}+2+&+-3\\+-5+&+8+\end{bmatrix}=\begin{bmatrix}+9+&+-14\\+-5+&+8+\end{bmatrix}$

7. Penyelesaian Sistem Persamaan Linear dengan Matriks

Matriks sanggup dipakai untuk mempermudah dalam menentukan penyelesaian sistem persamaan linear. Pada pembahasan kali ini, kita akan menggunakannya untuk menuntaskan sistem persamaan linear dua variabel dan tiga variabel.

7.1. Sistem Persamaan Linear Dua Variabel

Bentuk umum sistem persamaan linear dua variabel adalah

ax + by = p ............................................................................ (1)
cx + dy = q ............................................................................. (2)

Persamaan (1) dan (2) di atas sanggup kita susun ke dalam bentuk matriks menyerupai di bawah ini.
$+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}\begin{bmatrix}+x\\+y+\end{bmatrix}=\begin{bmatrix}+p\\+q+\end{bmatrix}$
Tujuan penyelesaian sistem persamaan linear dua variabel ialah menentukan nilai x dan y yang memenuhi sistem persamaan itu. Oleh sebab itu, berdasarkan penyelesaian matriks bentuk AX = B sanggup dirumuskan sebagai berikut.

$+\begin{bmatrix}+x\\+y+\end{bmatrix}=\frac{1}{ad-bc}\begin{bmatrix}+d+&+-b\\+-c+&+a+\end{bmatrix}=\begin{bmatrix}+p\\+q+\end{bmatrix}$

asalkan ad – bc ≠ 0.

Contoh Soal 23

Tentukan penyelesaian dari sistem persamaan linear berikut dengan cara matriks.

2x + y = 7
x + 3y = 7

Jawaban 23

Dari persamaan di atas sanggup kita susun menjadi bentuk matriks sebagai berikut.
$+\begin{bmatrix}+2+&+1\\+1+&+3+\end{bmatrix}\begin{bmatrix}+x\\+y+\end{bmatrix}=\begin{bmatrix}+4\\+7+\end{bmatrix}$
Dengan memakai rumus klarifikasi persamaan matriks di atas, diperoleh sebagai berikut.

Jadi, diperoleh penyelesaian x = 1 dan y = 2.

7.2. Sistem Persamaan Linear Tiga Variabel

Kalian tentu tahu bahwa untuk menuntaskan sistem persamaan linear tiga variabel sanggup dilakukan dengan beberapa cara, contohnya eliminasi, substitusi, adonan antara eliminasi dan substitusi, operasi baris elementer, serta memakai invers matriks. Kalian sanggup memakai cara-cara tersebut dengan bebas yang berdasarkan kalian paling efisien dan paling mudah.

Misalkan diberikan sistem persamaan linear tiga variabel berikut.

a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃

Sistem persamaan linear di atas sanggup kita susun ke dalam bentuk matriks menyerupai berikut.
$+\begin{bmatrix}+a_{1}+&+b_{1}+&+c_{1}\\+a_{2}+&+b_{2}+&+c_{2}\\+a_{3}+&+b_{3}+&+c_{3}+\end{bmatrix}\begin{bmatrix}+x\\+y\\+z+\end{bmatrix}=\begin{bmatrix}+d_{1}\\+d_{2}\\+d_{3}+\end{bmatrix}$

Misalkan A = $+\begin{bmatrix}+a_{1}+&+b_{1}+&+c_{1}\\+a_{2}+&+b_{2}+&+c_{2}\\+a_{3}+&+b_{3}+&+c_{3}+\end{bmatrix}$ , X = $+\begin{bmatrix}+x\\+y\\+z+\end{bmatrix}$ , dan B = $+\begin{bmatrix}+d_{1}\\+d_{2}\\+d_{3}+\end{bmatrix}$

Bentuk di atas sanggup kita tuliskan sebagai AX = B.
Penyelesaian sistem persamaan AX = B ialah X = A^-1 B. Dalam hal ini, A^-1 = $+\frac{1}{det\:+A}\:+adj\left+(+A+\right+)$

Oleh sebab itu, diperoleh :
$+X=\left+(\frac{1}{det\:+A}\:+adj\left+(+A+\right+)+\right+)B=\frac{1}{det\:+A}\:+adj\left+(A+\right+)B$

asalkan det A ≠ 0.

Contoh Soal 24

Tentukan himpunan penyelesaian dari sistem persamaan berikut.

2x + y – z = 1
x + y + z = 6
x – 2y + z = 0

Jawaban 24

Cara 1:

Operasi elemen baris, selain sanggup dipakai untuk mencari invers matriks, sanggup pula dipakai untuk menuntaskan sistem persamaan linear.

Dengan memakai operasi baris elementer.

Dengan demikian, diperoleh y = 2. Kita substitusikan nilai y = 2 ke persamaan (2) sehingga :

y + 3z = 11 ↔ 2 + 3z = 11
↔ 3z = 11 – 2
↔ 3z = 9
↔ z = 3

Substitusikan y = 2 dan z = 3 ke persamaan (1) sehingga diperoleh :

x + y + z = 6 ↔ x + 2 + 3 = 6
↔ x + 5 = 6
↔ x = 6 – 5
↔ x = 1

Jadi, penyelesaiannya ialah x = 1, y = 2, dan z = 3.

Dengan demikian, himpunan penyelesaiannya ialah {(1, 2, 3)}.

Cara 2:

Sistem persamaan linear di atas sanggup kita susun ke dalam bentuk matriks sebagai berikut.
Misalkan A = $+\begin{bmatrix}+2+&+1&-1\\+1+&+1&1\\+1+&+-2&1+\end{bmatrix}$ , X = $+\begin{bmatrix}+x\\+y\\+z+\end{bmatrix}$ , dan B = $+\begin{bmatrix}+1\\+6\\+0+\end{bmatrix}$

Dengan memakai minor-kofaktor, diperoleh :

det A = $+2\begin{bmatrix}+1+&+1\\+-2+&+1+\end{bmatrix}-1\begin{bmatrix}+1+&+1\\+1+&+1+\end{bmatrix}+\left+(+-1+\right+)\begin{bmatrix}+1+&+1\\+1+&+-2+\end{bmatrix}$

det A = 2(3) – 1(0) + (–1)(–3) = 9

Dengan memakai minor-kofaktor, diperoleh :

Dengan cara yang sama, kalian akan memperoleh K₃₁ = 2, K₃₂ = –3, dan K₃₃ = 1 (coba tunjukkan).

Dengan demikian, diperoleh :
kof(A) = $+\begin{bmatrix}+K_{11}+&+K_{12}&+K_{13}\\+K_{21}+&+K_{22}&+K_{23}\\+K_{31}+&+K_{32}&+K_{33}+\end{bmatrix}=\begin{bmatrix}+3+&+0&+-3\\+1+&+3&+5\\+2+&+-3&+1+\end{bmatrix}$

Oleh sebab itu, adj(A) = (kof(A))^T.
Adj(A) = $+\begin{bmatrix}+3+&+0&+-3\\+1+&+3&+5\\+2+&+-3&+1+\end{bmatrix}^{T}=\begin{bmatrix}+3+&+1&+2\\+0+&+3&+-3\\+-3+&+5&+1+\end{bmatrix}$
Jadi, X = $+\frac{1}{det\:+A}Adj\left+(+A+\right+)B$

Jadi, diperoleh x = 1, y = 2, dan z = 3. Dengan demikian, himpunan penyelesaian sistem persamaan di atas ialah {(1, 2, 3)}.

7.3. Menyelesaikan Sistem Persamaan Linear dengan Determinan

Sistem persamaan linear yang disusun dalam bentuk matriks juga sanggup ditentukan himpunan penyelesaiannya dengan metode determinan. Misalnya, sistem persamaan linear untuk dua variabel dan tiga variabel ialah sebagai berikut.

a. ax + by = p
cx + dy = q

b. a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃
Pada sistem persaman linear dua variabel, bentuk tersebut sanggup diubah ke bentuk matriks berikut.

$+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}\begin{bmatrix}+x\\+y+\end{bmatrix}=\begin{bmatrix}+p\\+q+\end{bmatrix}$ , dengan A = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ , X = $+\begin{bmatrix}+x\\+y+\end{bmatrix}$ , dan B = $+\begin{bmatrix}+p\\+q+\end{bmatrix}$ .

D = $+\begin{bmatrix}+a+&+b\\+c+&+d+\end{bmatrix}$ = ad – bc (Determinan koefisien x dan y, dengan elemen-elemen matriks A)

Dx = $+\begin{bmatrix}+p+&+b\\+q+&+d+\end{bmatrix}$ = pd – bq (Ganti kolom ke-1, dengan elemen-elemen matriks B)

Dy = $+\begin{bmatrix}+a+&+p\\+c+&+q+\end{bmatrix}$ = aq – cp (Ganti kolom ke-2, dengan elemen-elemen matriks B)

Nilai x dan y sanggup ditentukan dengan rumus berikut.
$+x=\frac{D_{x}}{D};\:+y=\frac{D_{y}}{D}$
Dengan cara yang sama sanggup ditentukan D, D_x, D_y, dan D_z untuk sistem persamaan linear tiga variabel sebagai berikut.

Nilai x, y, dan z sanggup ditentukan dengan cara berikut.

Contoh Soal 25

Tentukan penyelesaian sistem persamaan linear berikut dengan metode determinan.

a. 2x + y = 4
x – 2y = –3

b. x + y + z = 0
x + y – z = –2
x – y + z = 4

Penyelesaian 25

a. Sistem persamaan linear di atas sanggup disusun dalam bentuk matriks berikut.
$+\begin{bmatrix}+2+&+1\\+1+&+-2+\end{bmatrix}\begin{bmatrix}+x\\+y+\end{bmatrix}=\begin{bmatrix}+4\\+-3+\end{bmatrix}$

Kita tentukan nilai D, D_x, D_y .
D = $+\begin{bmatrix}+2+&+1\\+1+&+-2+\end{bmatrix}$ = – 4 – 1 = – 5
Dx = $+\begin{bmatrix}+4+&+1\\+-3+&+-2+\end{bmatrix}$ = – 8 – (–3) = – 5
Dy = $+\begin{bmatrix}+2+&+4\\+1+&+-3+\end{bmatrix}$ = – 6 – 4 = – 10
Jadi, x = $+\frac{D_{x}}{D}$ = $+\frac{-5}{-5}$ = 1 dan y = $+\frac{D_{y}}{D}$ = $+\frac{-10}{-5}$ = 2.

b. Sistem persamaan linear tiga variabel di atas sanggup disusun dalam bentuk matriks berikut.

Anda kini sudah mengetahui Matriks. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Yuana, R. A. 2009. Khazanah Matematika 3 : untuk Kelas XII Sekolah Menengan Atas / MA Program Ilmu Pengetahuan. Sosial. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 240.