Pintar Pelajaran Penyajian Data Statistik Dalam Bentuk Tabel, Diagram Batang, Garis, Lingkaran, Tabel Distribusi Frekuensi, Relatif Dan Kumulatif, Histogram, Poligon Frekuensi, Dan Ogive, Referensi Soal, Jawaban, Matematika

Penyajian Data Statistik dalam Bentuk Tabel, Diagram Batang, Garis, Lingkaran, Tabel Distribusi Frekuensi, Relatif dan Kumulatif, Histogram, Poligon Frekuensi, dan Ogive, Contoh Soal, Jawaban, Matematika - Ada dua cara penyajian data yang sering dilakukan, yaitu :

a) daftar atau tabel,

b) grafik atau diagram.

1. Penyajian Data dalam Bentuk Tabel

Misalkan, hasil ulangan Bahasa Indonesia 37 siswa kelas XI Sekolah Menengan Atas 3 disajikan dalam tabel di bawah. Penyajian data pada Tabel 1.1 dinamakan penyajian data sederhana. Dari tabel 1.1, Anda sanggup memilih banyak siswa yang menerima nilai 9, yaitu sebanyak 7 orang. Berapa orang siswa yang menerima nilai 5? Nilai berapakah yang paling banyak diperoleh siswa?

Jika data hasil ulangan bahasa Indonesia itu disajikan dengan cara mengelompokkan data nilai siswa, diperoleh tabel frekuensi berkelompok mirip pada Tabel 2.. Tabel 2. dinamakan Tabel Distribusi Frekuensi.

Tabel 1. Penyajian data sederhana

Nilai	Frekuensi
2	7
4	3
5	5
6	4
7	10
9	7
10	1

Tabel 2. Tabel Distribusi Frekuensi

Interval Kelas	Turus	Frekuensi
1–2	EB	7
3–4	C	3
5–6	EC	8
7–8	EE	10
9–10	EC	8
	Jumlah	37

2. Penyajian Data dalam Bentuk Diagram

Kerapkali data yang disajikan dalam bentuk tabel sulit untuk dipahami. Lain halnya kalau data tersebut disajikan dalam bentuk diagram maka Anda akan sanggup lebih cepat memahami data itu. Diagram yaitu gambar yang menyajikan data secara visual yang biasanya berasal dari tabel yang telah dibuat. Meskipun demikian, diagram masih mempunyai kelemahan, yaitu pada umumnya diagram tidak sanggup menawarkan citra yang lebih detail.

2.1. Diagram Batang

Diagram batang biasanya digunakan untuk menggambarkan data diskrit (data cacahan). Diagram batang yaitu bentuk penyajian data statistik dalam bentuk batang yang dicatat dalam interval tertentu pada bidang cartesius.

Ada dua jenis diagram batang, yaitu

1. diagram batang vertikal, dan
2. diagram batang horizontal.

Contoh Soal 1

Selama 1 tahun, toko "Anggo" mencatat laba setiap bulan sebagai berikut.

Tabel 3. Keuntungan Toko "Anggo" per Bulan (dalam jutaan rupiah)

Bulan ke	2,5	1,8	2,6	4,2	3,5	3,3	4,0	5,0	2,0	4,2	6,2	6,2
Keuntungan	1	2	3	4	5	6	7	8	9	10	11	12

a. Buatlah diagram batang vertikal dari data tersebut.

b. Berapakah laba terbesar yang diperoleh Toko "Anggo" selama 1 tahun?

c. Kapan Toko "Anggo" memperoleh laba yang sama selama dua bulan berturut-turut?

Penyelesaian 1

a. Diagram batang vertikal dari data tersebut, tampak pada gambar berikut.

Gambar 1. Diagram batang vertikal Keuntungan Toko "Anggo" per Bulan (dalam jura rupiah)

b. Dari diagram tersebut tampak bahwa laba terbesar yang diperoleh Toko "Anggo" selama 1 tahun yaitu sebesar Rp 6.200.000,00.

c. Toko "Anggo" memperoleh laba yang sama selama dua bulan beturut-turut pada bulan ke-11 dan ke-12.

2.2. Diagram Garis

Pernahkah Anda melihat grafik nilai tukar dolar terhadap rupiah atau pergerakan saham di TV? Grafik yang mirip itu disebut diagram garis. Diagram garis biasanya digunakan untuk menggambarkan data ihwal m keadaan yang berkesinambungan (sekumpulan data kontinu). Misalnya, jumlah penduduk setiap tahun, perkembangan berat tubuh bayi setiap bulan, dan suhu tubuh pasien setiap jam.

Seperti halnya diagram batang, diagram garis pun memerlukan sistem sumbu datar (horizontal) dan sumbu tegak (vertikal) yang saling berpotongan tegak lurus. Sumbu mendatar biasanya menyatakan jenis data, contohnya waktu dan berat. Adapun sumbu tegaknya menyatakan frekuensi data. Langkah-langkah yang dilakukan untuk menciptakan diagram garis yaitu sebagai berikut.

1. Buatlah suatu koordinat (berbentuk bilangan) dengan sumbu mendatar memperlihatkan waktu dan sumbu tegak memperlihatkan data pengamatan.
2. Gambarlah titik koordinat yang memperlihatkan data pengamatan pada waktu t.
3. Secara berurutan sesuai dengan waktu, hubungkan titiktitik koordinat tersebut dengan garis lurus.

Contoh Soal 2

Berikut ini yaitu tabel berat tubuh seorang bayi yang dipantau semenjak lahir hingga berusia 9 bulan.

Usia (bulan)	3,5	4	5,2	6,4	6,8	7,5	7,5	8	8,8	8,6
Berat Badan (kg)	0	1	2	3	4	5	6	7	8	9

a. Buatlah diagram garisnya.

b. Pada usia berapa bulan berat badannya menurun?

c. Pada usia berapa bulan berat badannya tetap?

Pembahasan 2

a. Langkah ke-1

Buatlah sumbu mendatar yang memperlihatkan usia anak (dalam bulan) dan sumbu tegak yang memperlihatkan berat tubuh anak (dalam kg).

Langkah ke-2

Gambarlah titik koordinat yang memperlihatkan data pengamatan pada waktu t bulan.

Langkah ke-3

Secara berurutan sesuai dengan waktu, hubungkan titik-titik koordinat tersebut dengan garis lurus.

Dari ketiga langkah tersebut, diperoleh diagram garis dari data tersebut tampak pada Gambar 2.

Gambar 2. Diagram garis berat tubuh bayi semenjak usia 0 bulan–9 bulan

b. Dari diagram tersebut sanggup dilihat bahwa berat tubuh bayi menurun pada usai 8 hingga 9 bulan.

c. Berat tubuh bayi tetap pada usia 5 hingga 6 bulan. Darimana Anda memperoleh hasil ini? Jelaskan.

Observasi: Interpolasi dan Ekstrapolasi Data

Anda sanggup melaksanakan observasi terhadap kecenderungan data yang disajikan pada suatu diagram garis. Dari observasi ini, Anda sanggup menciptakan perkiraan-perkiraan dengan cara interpolasi dan ekstrapolasi. Hal ini ditempuh dengan mengganti garis patah pada diagram garis menjadi garis lurus. Interpolasi data yaitu menaksir data atau memperkirakan data di antara dua keadaan (misalnya waktu) yang berurutan. Misalkan, dari gambar grafik Contoh soal 2. sanggup diperkirakan berat tubuh bayi pada usia 5,5 bulan. Coba Anda amati grafik tersebut, kemudian tentukan berat tubuh bayi pada usia 5,5 bulan.

Ekstrapolasi data yaitu menaksir atau memperkirakan data untuk keadaan (waktu) mendatang. Cara yang sanggup dilakukan untuk ekstrapolasi yaitu dengan memperpanjang ruas garis terujung ke arah kanan. Misalkan, dari gambar grafik soal 2. sanggup diperkirakan berat tubuh bayi pada usia 10 bulan. Jika garis lurus sudah ditentukan, Anda sanggup memilih interpolasi data. Untuk ekstrapolasi data, Anda harus berhati-hati. Menurut diagram garis, berapa kira-kira berat tubuh bayi pada usia 10 bulan? Berikan alasan Anda.

2.3. Diagram Lingkaran

Untuk mengetahui perbandingan suatu data terhadap keseluruhan, suatu data lebih sempurna disajikan dalam bentuk diagram lingkaran. Diagram lingkaran yaitu bentuk penyajian data statistika dalam bentuk lingkaran yang dibagi menjadi beberapa juring lingkaran.

Langkah-langkah untuk menciptakan diagram lingkaran yaitu sebagai berikut.

1. Buatlah sebuah lingkaran pada kertas.
2. Bagilah lingkaran tersebut menjadi beberapa juring lingkaran untuk menggambarkan kategori yang datanya
3. telah diubah ke dalam derajat.

Agar lebih jelasnya, pelajarilah pola berikut.

Contoh Soal 3

Tabel berikut memperlihatkan banyaknya siswa di suatu kabupaten berdasarkan tingkat sekolah pada tahun 2007.

Tingkat Pendidikan	Banyaknya Siswa
SD SMP SMA	175 600  225

a. Buatlah diagram lingkaran untuk data tersebut.

b. Berapa persen siswa yang menuntaskan sekolah hingga pada tingkat SMP?

c. Berapa persen siswa yang menuntaskan sekolah hingga pada tingkat SMA?

Pembahasan 3

a. Jumlah seluruh siswa yaitu 1.000 orang. Seluruh siswa diklasifikasikan menjadi 5 katagori: SD = 175 orang, Sekolah Menengah Pertama = 600 orang, dan Sekolah Menengan Atas = 225 orang.

• Siswa SD = (175/1.000) x 100% = 17,5%

Besar sudut sektor lingkaran = 17,5% × 360° = 63°

• Siswa Sekolah Menengah Pertama = (600/1.000) x 100% = 60%

Besar sudut sektor lingkaran = 60% × 360° = 216°

• Siswa SMA= (225/1.000) 100% = 22,5%

Besar sudut sektor lingkaran = 22,5% × 360° = 81°

Diagram lingkaran ditunjukkan pada Gambar 3.

Gambar 3. Diagram lingkaran banyaknya siswa di suatu kabupaten berdasarkan tingkat sekolah pada tahun 2007

b. Persentase siswa yang menuntaskan sekolah hingga pada tingkat Sekolah Menengah Pertama yaitu 60%.

c. Persentase siswa yang menuntaskan sekolah hingga pada tingkat SMAadalah 22,5%.

3. Tabel Distribusi Frekuensi, Frekuensi Relatif dan Kumulatif, Histogram, Poligon Frekuensi, dan Ogive

3.1. Tabel Distribusi Frekuensi

Data yang berukuran besar (n > 30) lebih sempurna disajikan dalam tabel distribusi frekuensi, yaitu cara penyajian data yang datanya disusun dalam kelas-kelas tertentu.

Langkah-langkah penyusunan tabel distribusi frekuensi yaitu sebagai berikut.

• Langkah ke-2 memilih banyak interval (K) dengan rumus "Sturgess" yaitu: K= 1 + 3,3 log n dengan n yaitu banyak data. Banyak kelas harus merupakan bilangan bundar positif hasil pembulatan.

• Langkah ke-3 memilih panjang interval kelas (I) dengan memakai rumus:

I = J/K

• Langkah ke-4 memilih batas-batas kelas. Data terkecil harus merupakan batas bawah interval kelas pertama atau data terbesar yaitu batas atas interval kelas terakhir.

• Langkah ke-5 memasukkan data ke dalam kelas-kelas yang sesuai dan memilih nilai frekuensi setiap kelas dengan sistem turus.

• Menuliskan turus-turus dalambilangan yang bersesuaian dengan banyak turus.

Ingatlah :

Menentukan banyak kelas interval dengan hukum Sturges dimaksudkan semoga interval tidak terlalu besar lantaran jadinya akan menyimpang dari keadaan sesungguhnya. Sebaiknya, kalau interval terlalu kecil, jadinya tidak menggambarkan keadaan yang diharapkan.

Contoh Soal 4

Seorang peneliti mengadakan penelitian ihwal berat tubuh dari 35 orang.

Data hasil penelitian itu (dalam kg) diberikan berikut ini:

48 32 46 27 43 46 25 41 40 58 16 36

21 42 47 55 60 58 46 44 63 66 28 56

50 21 56 55 25 74 43 37 51 53 39

Sajikan data tersebut ke dalam tabel distribusi frekuensi.

Jawaban 4

1. Jangkauan (J) = Xm- Xn = 74 – 16 = 58.

2. Banyak kelas (K) = 1 + 3,3 log n = 1 + 3,3 log 35 = 6,095. Banyak kelas dibulatkan menjadi "6".

3. Panjang interval kelas (I) yaitu I = J/K = 58/6 = 9,67. Panjang interval kelas dibulatkan menjadi "10". 

Dengan panjang interval kelas = 10 dan banyak kelas = 6, diperoleh tabel distribusi frekuensi mirip pada Tabel 4. atau Tabel 5

Cara I: Batas bawah kelas pertama diambil datum terkecil. Amati Tabel 4. Dari tabel tersebut tampak bahwa frekuensi paling banyak dalam interval 46–55. Artinya, berat tubuh kebanyakan berkisar antara 46 kg dan 55 kg.

Tabel 4. Tabel distribusi frekuensi

Interval Kelas	Turus	Frekuensi
16–25	E	5
26–35	C	3
36–45	ED	9
46–55	EE	10
56–65	EA	6
66–75	B	2
	Jumlah	35

Cara II: Batas atas kelas terakhir diambil datum terbesar. Amati Tabel 5.

Tabel 5. Tabel distribusi frekuensi

Interval Kelas	Turus	Frekuensi
15–24	C	3
25–34	E	5
35–44	ED	9
45–54	EC	8
55–64	EC	8
65–74	B	2
	Jumlah	35

Dari tabel tampak frekuensi paling sedikit dalam interval 65–74. Artinya, berat tubuh antara 65 kg dan 74 kg ada 2 orang. Perhatikan interval kelas yang pertama, yaitu 15–24. 15 disebut batas bawah dan 24 disebut batas atas. Ukuran 15–24 yaitu hasil pembulatan, ukuran yang gotong royong terletak pada 14,5–24,5. 14,5 disebut tepi bawah kelas (batas bawah nyata) dan 24,5 disebut tepi atas kelas (batas atas nyata) pada interval kelas 15–24.

Dalam memilih tepi bawah kelas dan tepi atas kelas pada setiap interval kelas, harus diketahui satuan yang dipakai. Dengan demikian, untuk tepi bawah kelas yaitu batas bawah kelas dikurangi 1/2 satuan ukuran. Jadi, tepi kelas dari interval kelas 15–24 menjadi 14,5–24,5.

3.2. Frekuensi Relatif dan Kumulatif

Frekuensi yang dimiliki setiap kelas pada tabel distribusi frekuensi bersifat mutlak. Adapun frekuensi relatif dari suatu data yaitu dengan membandingkan frekuensi pada interval kelas itu dengan banyak data dinyatakan dalam persen. Contoh: interval frekuensi kelas yaitu 20. Total data seluruh interval kelas = 80 maka frekuensi relatif kelas ini yaitu 20/8 = ¼, sedangkan frekuensi relatifnya adalah ¼ × 100% = 25%.

Dari uraian tersebut, dapatkah Anda menyatakan rumus frekuensi relatif? Cobalah nyatakan rumus frekuensi relatif dengan kata-kata Anda sendiri.

Frekuensi relatif dirumuskan sebagai berikut.

Frekuensi relatif kelas ke-k = frekuensi kelas ke-k / banyak data

Frekuensi kumulatif kelas ke-k yaitu jumlah frekuensi pada kelas yang dimaksud dengan frekuensi kelas-kelas sebelumnya.

Ada dua macam frekuensi kumulatif, yaitu

1. frekuensi kumulatif "kurang dari" ("kurang dari" diambil terhadap tepi atas kelas);
2. frekuensi kumulatif "lebih dari" ("lebih dari" diambil terhadap tepi bawah kelas).

Tepi atas = batas atas + ½ satuan pengukuran

Tepi bawah = batas bawah - ½ satuan pengukuran

Contoh Soal 5

Dari Tabel 4. untuk interval kelas 46 – 55 (kelas 4), hitunglah

a. frekuensi relatif;

b. frekuensi kumulatif "kurang dari";

c. frekuensi kumulatif "lebih dari".

Penyelesaian 5

a. Frekuensi relatif kelas ke-4 = (frekuensi kelas ke-4 / banyak datum) x 100 % = 10/35 x 100% = 28,57%

b. Frekuensi kumulatif "kurang dari" untuk interval kelas 46 – 55

= 5 + 3 + 9 + 10 = 27 (kurang dari tepi atas kelas 55,5)

c. Frekuensi kumulatif "lebih dari" untuk interval kelas 46 – 55

= 10 + 6 + 2 = 18 (lebih dari tepi bawah kelas 45,5).

3.3. Histogram dan Poligon Frekuensi

Histogram merupakan diagram frekuensi bertangga yang bentuknya mirip diagram batang. Batang yang berdekatan harus berimpit. Untuk pembuatan histogram, pada setiap interval kelas diharapkan tepi-tepi kelas. Tepi-tepi kelas ini digunakan unntuk memilih titik tengah kelas yang sanggup ditulis sebagai berikut.

Titik tengah kelas = ½ (tepi atas kelas + tepi bawah kelas)

Poligon frekuensi sanggup dibentuk dengan menghubungkan titik-titik tengah setiap puncak persegipanjang dari histogram secara berurutan. Agar poligon "tertutup" maka sebelum kelas paling bawah dan sehabis kelas paling atas, masing-masing ditambah satu kelas.

Contoh Soal 6

Tabel distribusi frekuensi hasil ujian matematika Kelas XI Sekolah Menengan Atas Cendekia di Kalimantan Barat diberikan pada Tabel 6. Buatlah histogram dan poligon frekuensinya.

Tabel 6. Tabel distribusi frekuensi hasil ujian matematika Kelas XI Sekolah Menengan Atas Cendekia di Kalimantan Barat

Kelas Interval	Frekuensi
21–30	2
31–40	3
41–50	11
51–60	20
61–70	33
71–80	24
81–90	7
	100

Jawaban 6

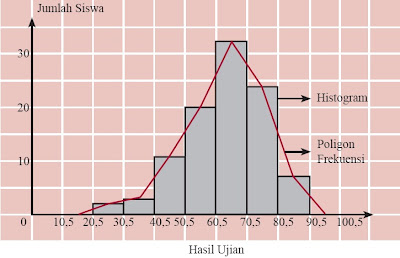Gambar 4. Histogram hasil ujian matematika Kelas XI Sekolah Menengan Atas Cendekia di Kalimantan Barat.

Dari histogram tersebut tampak bahwa kebanyakan siswa memperoleh nilai antara 60,5 dan 70,5. Coba Anda ceritakan hal lain dari histogram tersebut.

3.4. Ogive (Ogif)

Grafik yang memperlihatkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari dinamakan poligon kumulatif.

Untuk populasi yang besar, poligon mempunyai banyak ruas garis patah yang ibarat kurva sehingga poligon frekuensi kumulatif dibentuk mulus, yang jadinya disebut ogif.

Ada dua macam ogif, yaitu sebagai berikut.

a. Ogif dari frekuensi kumulatif kurang dari disebut ogif positif.

b. Ogif dari frekuensi kumulatif lebih dari disebut ogif negatif.

Contoh Soal 7

Tabel 7. dan 8. berturut-turut yaitu tabel distribusi frekuensi kumulatif "kurang dari" dan "lebih dari" ihwal nilai ulangan Biologi Kelas XI Sekolah Menengan Atas 3.

Tabel 7. Tabel distribusi frekuensi kumulatif "kurang dari" ihwal nilai ulangan Biologi Kelas XI Sekolah Menengan Atas 3.

Nilai	Frekuensi
< 20,5	0
< 30,5	2
< 40,5	5
< 50,5	16
< 60,5	36
< 70,5	69
< 80,5	93
< 90,5	100

Tabel 8. Tabel distribusi frekuensi kumulatif "lebih dari" tentang nilai ulangan Biologi Kelas XI Sekolah Menengan Atas 3.

Nilai	Frekuensi
> 20,5	100
> 30,5	98
> 40,5	95
> 50,5	84
> 60,5	64
> 70,5	31
> 80,5	7
> 90,5	0

a. Buatlah ogif positif dan ogif negatif dari tabel tersebut.

b. Berapakah jumlah siswa yang mempunyai nilai Biologi kurang dari 85?

c. Berapakah jumlah siswa yang mempunyai berat tubuh lebih dari 40?

Pembahasan 8

a. Ogif positif dan ogif negatif dari tabel tersebut tampak pada gambar 5.

Gambar 5. Kurva ogif positif dan negatif nilai ulangan Biologi Kelas XI Sekolah Menengan Atas 3.

b. Dari kurva ogif positif, tampak siswa yang mempunyai nilai kurang dari 85 yaitu sebanyak 93 orang.

c. Dari kurva ogif negatif, tampak siswa yang mempunyai nilai lebih dari 40 yaitu sebanyak 96 orang.

Anda kini sudah mengetahui Penyajian Data Statistik. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.

Share this post