Garis Tinggi Dan Garis Berat Pada Segitiga

Garis-garis istimewa pada segitiga terdiri dari garis tinggi, garis bagi, garis sumbu, dan garis berat. Garis tinggi pada suatu sisi dari suatu segitiga yakni garis yang ditarik dari sebuah titik sudut segitiga dan tegaklurus sisi di depannya. Garis bagi pada suatu segitiga yakni garis yang ditarik dari titik sudut segitiga dan membagi sudut tersebut menjadi dua sama besar. Garis sumbu pada suatu sisi dari suatu segitiga yakni garis yang tegak lurus dan melalui titik tengah sisi tersebut. Garis berat pada suatu sisi dari suatu segitiga yakni garis yang menghubungkan titik sudut dihadapan sisi itu dengan titik tengah sisi itu.

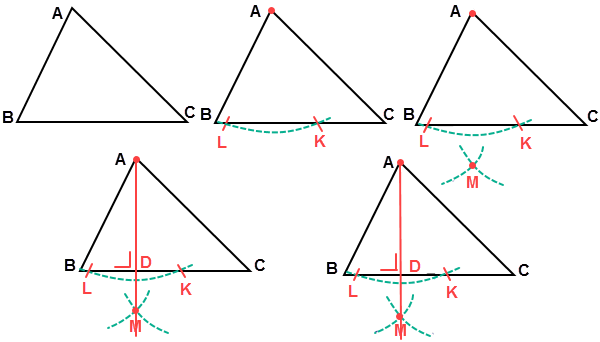
A . Melukis Garis Tinggi pada Segitiga
Panjang garis tinggi sanggup dihitung dengan mengetahui Luas segitiga. Lalu, dengan menggunakan rumus Luas = 1/2.a. t, maka tentunya tinggi segitiga (t) sanggup diketahui Untuk melukis garis tinggi pada segitiga sanggup dilakukan dengan cara sebagai berikut.


Gambarlah segitiga ABC sebarang Buatlah busur bulat dari titik A sebgai titik sentra sehingga busur bulat tersebut memotong garis BC di titik K dan L Buatlah busur dari titik K dan L sebagai titik sentra dengan jari-jari yang sama panjang, sehingga kedua busur tersebut berpotongan di titik M Hubungkan titik A dengan titik M, sehingga memotong garis BC di titik D Jadi, garis AD yakni Garis Tinggi Segitiga pada sisi BC

B . Melukis Garis Bagi pada Segitiga
Garis bagi dalam yakni garis yang melalui titik sudut segitiga dan membagi kedua sudut di sebelahnya sama besar. Garis ini terletak dalam segitiga. Untuk melukis garis bagi pada segitiga sanggup dilakukan dengan cara sebagai berikut.


Gambarlah segitiga ABC sebarang Buatlah busur dari titik sebagai titik sentra sehingga busur tersebut memotong garis AB di titik K dan garis AC di ttik L Buatlah dua busur dari titik K dan L sebagai titik sentra dengan panjang jari-jari yang sama, sehingga kedua busur tersebut berpotongan di titik M Hubungkan titik A dengan titik M, sehingga memotong garis AC di titik D Jadi, garis AD yakni Garis Bagi Segitiga pada sisi BC

C. Melukis Garis Sumbu pada Segitiga
Garis sumbu yakni garis yang melalui titik tengah suatu sisi segitiga dan tegak lurus terhadap sisi itu. Ketiga garis sumbu bertemu di satu titik yang dinamakan circumcenter. titik tersebut merupakan sentra bulat luar segitiga (circumcircle). Untuk melukis garis sumbu pada segitiga sanggup dilakukan dengan cara sebagai berikut.


Gambarlah segitiga ABC sebarang Buatlah busur bulat dengan titik B sebagai titik sentra dan jari-jari lebih setengah dari sisi BC sehingga busurnya di atas dan di bawah garis BC Buatlah busur bulat dengan titik C sebagai titik sentra dan jari-jari tetap sama ibarat busur yang titik pusatnya di titik B sehingga memotong kedua busur di titik P dan Q Hubungkan titik P dengan titik Q, maka garis PQ yakni garis sumbu pada sisi BC

D . Melukis Garis Berat pada Segitiga
Garis berat yakni garis yang terhubung dari titik sudut suatu segitiga ke titik tengah sisi yang berlawanan. Hal ini menjadikan tempat yang terbagi oleh garis berat menjadi sama luasnya. Untuk melukis garis berat pada segitiga sanggup dilakukan dengan cara sebagai berikut.


Gambarlah segitiga ABC sebarang Buatlah garis sumbu pada garis BC yang memotonga sisi BC di titik D Hubungkan titik A dengan titik D Garis AD merupakan garis berat, sehingga panjang garis BD = DC

Ayo Kita Berlatih
Kerjakan soal-soal berikut.
1. Dengan menggunakan jangka dan penggaris, salin dan lukislah garis yang tegak lurus CD melalui titik A berikut

garis istimewa pada segitiga terdiri dari garis tinggi Garis Tinggi dan Garis Berat Pada Segitiga

2. Gambarlah ABC siku-siku di titik A dengan AB = 6 cm dan AC = 5 cm. Kemudian lukislah ketiga garis berat pada ΔABC tersebut dan tentukan titik perpotongannya.

3. Gambarlah ΔDEF sama kaki dengan DE = DF. Lukislah ketiga garis sumbu pada segitiga tersebut.

4. Gambarlah segitiga tumpul KLM, kemudian lukislah ketiga garis tinggi pada segitiga tersebut.

5. Lukislah ketiga garis tinggi

a. pada segitiga lancip.
b. pada segitiga tumpul.
c. Kemudian apakah yang sanggup kalian simpulkan wacana ketiga garis tinggi pada suatu segitiga?
Garis tinggi pada suatu sisi dari suatu segitiga yakni garis yang ditarik dari sebuah titik sudut segitiga dan tegaklurus sisi di depannya.

6. Lukislah ketiga garis bagi

a. pada segitiga siku-siku.
b. pada segitiga tumpul.
c. Kemudian apakah yang sanggup kalian simpulkan wacana ketiga garis bagi pada suatu segitiga?
Garis bagi pada suatu segitiga yakni garis yang ditarik dari titik sudut segitiga dan membagi sudut tersebut menjadi dua sama besar.

7. a. Lukislah ketiga garis sumbu sisi-sisi segitiga ABC!
b. Apakah ketiga sumbu segitiga ABC saling berpotongan di satu titik?
c. Lukislah bulat dengan sentra pada titik potong ketiga sumbu dan melalui ketiga titik sudut segitiga.

8. Lukislah sebuah belahketupat yang panjang diagonalnya 6 cm dan 8 cm. Berapakah panjang sisi belahketupat dan berapakah luasnya?

9. Pada segitiga ABC (siku-siku di C), titik Q pada AC, titik P pada AB, dan PQ sejajar BC. Panjang sisi AQ = 3, AP = 5, BC = 8, maka luas ΔABC yakni … (OSK Sekolah Menengah Pertama 2010)

Karena PQ sejajar BC , maka besar sudut AQP = besar sudut ACB = 90°(pasangan sudut sehadap)
Segitiga AQP siku-siku di Q , maka panjang PQ = 4 (ingat tripel Pythagoras 3 , 4, 5). Begitu pula besar sudut APQ = besar sudut ABC (pasangan sudut sehadap), maka Segitiga AQP sebangun dengan segitiga ACB , (sd-sd-sd) akibatnya;