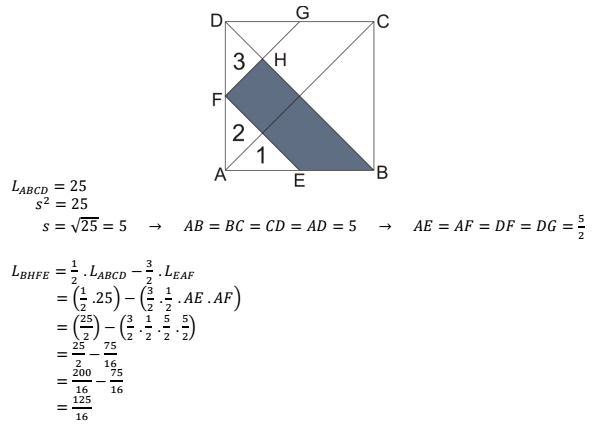Soal Penilaian Bahan 8 Segiempat Dan Segitiga
Sunday, March 22, 2020
Edit
Segi empat ialah suatu segi banyak (polygon) yang mempunyai empat sisi dan empat sudut. Segitiga ialah bangkit datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik sudut. Luas ialah besaran yang menyatakan ukuran dua dimensi suatu bab permukaan yang dibatasi dengan jelas, biasanya suatu kawasan yang dibatasi oleh kurva tertutup.
Persegipanjang ialah segi empat yang mempunyai dua pasang sisi sejajar dan sama panjang. Jika L ialah luas, K ialah keliling, p ialah panjang, dan l ialah lebar sebuah persegi panjang, maka: L = p × l dan K = 2p + 2l.
Persegi ialah persegipanjang yang semua sisinya sama panjang. Jika L ialah luas, K ialah keliling, r ialah sisi sebuah persegi, maka: L = r × r dan K = 4 × r.
Trapesium ialah segi empat yang mempunyai sempurna satu pasang sisi sejajar. Jika L ialah luas, K ialah keliling, b ialah panjang alas, a ialah sisi atas, t ialah tinggi sebuah trapesium, maka: L = a + b/2 ×t dan. K = jumlah seluruh panjang sisinya.
Jajargenjang ialah segiempat yang mempunyai dua pasang sisi sejajar dan sudut-sudut yang berhadapan sama besar. Misalkan L ialah luas, K ialah keliling, a ialah panjang alas, l ialah lebar, dan t ialah tinggi sebuah jajargenjang, maka: L = a x t.
Belahketupat ialah segiempat yang mempunyai dua pasang sisi sejajar dan kedua diagonal bidangnya saling tegak lurus. Sebuah belahketupat dengan panjang sisinya a dan panjang diagonal bidangnya d1 dan d2 maka luas dan kelilingnya berturut-turut adalah: L = 1/2 x d1 + d2 dan K = 4 × a.
Layang-layang ialah segiempat yang mempunyai dua pasang sisi yang sama panjang dan dua diagonal bidang yang saling tegak lurus. Sebuah layang-layang dengan panjang sisi s1 dan s2, serta panjang diagonalnya masing-masing d1 dan d2, maka luas dan kelilingnya berturut-turut adalah: L = 1/2 x d1 × d2 dan K = 2s1 + 2s2.
Terdapat beberapa jenis segitiga, yaitu: samasisi, segitiga samakaki, segitiga sebarang, segitiga siku-siku, segitiga tumpul, segitiga lancip. Jika L ialah luas, K ialah keliling, t ialah tinggi, a ialah bantalan sebuah segitiga, dan ketiga sisinya ialah p, q,dan r, maka: L = 1/2 (a × t) dan K = p + q + r.
A. Soal Pilihan Ganda
1. Jika suatu persegi mempunyai luas 144 cm², maka panjang sisinya sama dengan ... mm
144 cm persegi = 14.400 mm²
Sisinya = √14.400 mm² = 120 mm
2. Aisyah mempunyai sebuah kain yang berbentuk persegipanjang. Ia berencana menghias sekeliling kain tersebut dengan renda. Jika ternyata renda yang diharapkan Aisyah paling sedikit 450 cm, salah
satu ukuran kain yang dimiliki Aisyah ialah ...
K= 2(P+l)
450 cm = 2(p+l)
(p+l) = 450/2=225 cm
Perkiraan ukuran kain, ada beberapa kemungkinan,diantaranya
Panjang 125 dan Lebar 100 cm
3. Ukuran diagonal-diagonal suatu layang-layang yang mempunyai luas 640 cm² ialah ....
Luas layang-layang = 1/2 x d₁ x d₂
640 = 1/2 x d₁ x d₂
d₁ x d₂ = 1280
dari sini ukuran d₁ dan d₂ sanggup saja,
40 cm dan 32 cm,
80 cm dan 16 cm,
64 cm dan 20 cm,
4. Perhatikan gambar persegi panjang dan persegi berikut
Jika luas persegi panjang = 1/ 2 kali luas persegi, lebar persegi panjang tersebut ialah ....
Luas persegi panjang = 1/2 kali persegi
Luas persegi = 8,5 x 8,5 =72,25
Apabila 1/2 berarti 72,25 : 0,5 =36,125
Luas persegi panjang = 36,125 : 8,5 = 4,25 cm
Kaprikornus lebar persegi panjang ialah 4,25 cm
5. Banyak persegi pada Gambar berikut ialah ….
Tentukan banyaknya persegi yang terdiri dari 1 kotak, 4 kotak, 9 kotak, dan 16 kotak. Kemudian jumlahkan. Jadi, banyak persegi pada gambar tersebut ialah 55
6. Perhatikan gambar berikut. Bangun yang mempunyai luas terbesar ialah ....
7. Perhatikan gambar berikut.
Keliling bangkit pada gambar di atas ialah ....
8. Luas kawasan pada gambar di bawah ialah …..
Jawaban C.
9. Perhatikan gambar persegi ABCD dan persegi KLMN.
Jika B ialah titik sentra simetri putar persegi KLMN, maka luas kawasan yang diarsir ialah ...
10. Perhatikan gambar berikut.
Jika luas kawasan yang diarsir20 cm², luas kawasan yang tidak diarsir ialah ....
L persegi = s² = 10² = 100 cm²
L persegi panjang = p x l = 12 x 5 = 60 cm²
→ Luas kawasan tidak diarsir = (luas persegi + persegi panjang) - luas arsir
→ L total = (160 - 20) cm²
→ L = 140 cm²
11. Nilai panjang FB dari jajargenjang berikut ialah …
12. Perhatikan gambar berikut.
Luas jajargenjang ABCD pada gambar di atas ialah ...
13. Berdasarkan gambar berikut, nilai x ialah ....
14. Perhatikan gambar belahketupat ABCD.salah
∠A : ∠B = 1 : 2. Besar ∠C ialah ......
C = 60°
15. Perhatikan gambar di samping
Panjang AC adalah......
16. Perhatikan lukisan berikut.
Urutan cara melukis garis bagi pada gambar ΔKLM yang benar ialah ....
Garis bagi ialah garis yang ditarik dari suatu titik sudut yang membagi sudut tersebut menjadi dua bab yang sama. Pada gambar di atas, garis bagi ditarik dari titik sudut M. Cara melukis garis bagi tersebut ialah sebagai berikut.
Cara melukis garis bagi
Jadi, urutan cara melukis garis bagi pada segitiga tersebut ialah 3, 1, 2, 4 atau 3, 2, 1, 4 (D).
17. Gambar di bawah ini,
ΔABE, ΔBCF, ΔCDG, dan ΔADH mempunyai bentuk dan ukuran yang sama. Luas persegi ABCD sama dengan jumlah luas kawasan yang diarsir. Jika luas ABCD = 2M, maka luas
EFGH ialah ....
18. Jika luas satu persegi kecil ialah 4 m², maka luas bangkit datar pada gambar di bawah ialah ...
Gambar yang orisinil di geser ke kiri setengah kotak, lalu buatlah garis bantu yang berwarna merah. Sehingga terbentuk 4 segitiga, selanjutnya geserlah 2 segitiga bab atas kebagian bawah menyerupai pada gambar di atas. Jadi, maka luas bangkit datar pada gambar tersebut ialah 144 m²
19. Perhatikan gambar berikut.
Luas yang di arsir ialah ....
20. Suatu kardus polos dari kertas berbentuk kubus. Volume kardus ialah 64.000 cm³. Fitri memotong sempurna pada rusuk kubus dan mengambil dua sisi bab samping kardus tersebut. Fitri menciptakan garis pada satu potong sisi kardus dan diperolah satu segitiga siku-siku yang perbandingan dua sisi siku-siku ialah 1 : 2. Pada satu potongan sisi kardus yang lain dilukis satu segitiga sama kaki (lihat gambar). Jika ternyata dua segitiga ini sama luasnya, maka panjang sisi yang sama pada segitiga sama kaki ialah .... cm
Gunakan rumus pythagoras untuk mencari panjang s Jadi, panjang sisi yang sama pada segitiga sama kaki ialah 20√ 2cm
A. Soal Uraian
1. Misalkan suatu persegi diletakkan berimpit di kanan persegi yang lainnya. Tentukan keliling persegi yang terdiri dari:
a. 1 persegi. 4s
b. Gabungan 2 persegi. 6s
c. Gabungan 3 persegi. 8 s
d. Gabungan n persegi. (2n + 2)s
e. Berikan alasan yang dipakai untuk menggeneralisasi soal butir d.
Dengan memperhatikan referensi mulai keliling 1 persegi, 2 persegi, 3 persegi, dan seterusnya. Membentuk referensi bilangan genap yang dimulai dari bilangan 4, sehingga didapat untuk sebanyak n persegi = (2n + 2)s
2. Misalkan a merupakan bantalan jajar genjang PQRS dengan t merupakan tingginya. Jika 2t = 3a, tentukan:
a. panjang t dalam a. 2t = 3a. t = (3/2)a
b. panjang bantalan dan tingginya bila luas jajar genjang tersebut 864 cm².
L = a x t
864 = a x (3/2)a
864 = (3/2) a²
a² = 864 x 2/3
a² = 576
a = 24 Cm
t = (3/2)t
t = (3/2) x 24
t = 36
3. Diketahui keliling ΔKLM ialah 40 cm.
a. Berbentuk apakah ΔKLM ? Segitiga sama kaki
b. Tentukan panjang sisi ΔKLM !
KL = LM = 2x - 5 , KM = x
keliling = KL + LM + KM
=> (2x - 5) + (2x - 5) + x = 40
=> 5x - 10 = 40
=> 5x = 50
=> x = 10
KL = LM = 2x -5 = 2.10 - 5 = 15
KM = 10
4. Keliling segi-4 PQRS pada gambar di bawah ialah 22 cm.
a. Tentukan panjang PQ, SR, PS dan RQ! PQ, SR, PS dan RQ = 5,5 cm
b. Bagaimanakah caramu menghitung luas PQRS?
c. Berapakah luas PQRS? L=5,5 x 5,5 = 30,25 cm²
5. Diketahui bangun-bangun menyerupai berikut.
a. Tentukan luas dari tiap-tiap bangkit di atas.(a) 32 satuan, (b)24 satuan, dan (c) 20 satuan
b. Bangun manakah yang mempunyai luas terbesar? Bangun (a)
6. Perhatikan gambar berikut.
ABCD persegi dengan panjang sisi-sisinya ialah 2 cm. E ialah titik tengah CD dan F ialah titik tengah AD. Luas kawasan EDFGH adalah... cm².
Gunakan Teorema Pythagoras untuk memilih panjang AC. Perhatikan AP, PC, DP, dan PB. Kemudian perhatikan persegi kecil yang berada didalam persegi ABCD! Yaitu Terdiri dari 9 persegi kecil, sehingga garis AD membagi menjadi 3 bab yang sama besar, begitu juga panjang diagonal-diagonalnya membagi menjadi 3 bab yang sama besar,
Dapatkan Luas kawasan EDFGH = Luas persegi ABCD – 2Luas BCE – Luas ΔBHG.
Jadi, Luas kawasan EDFGH = 4/3 cm²
7. Perhatikan gambar di bawah.
Terdapat 4 buah layang-layang kongruen yang termuat pada persegi dan ternyata masih tersisa kawasan persegi yang diarsir. Jika panjang p = 3√ 2 cm, dan q = 5 √2 cm, maka luas kawasan yang diarsir ialah …. cm²
Carilah panjang p + q, luas persegi besar, luas segitiga ABC Dapatkan, Luas kawasan yang diarsir = Luas persegi – 8 Luas segitiga ABC Jadi, luas kawasan yang diarsir ialah 8 cm²
8. Diketahui luas persegi ABCD ialah 25 m2. Jika E, F, dan G masing-masing ialah titik tengah AB, AD, dan CD menyerupai pada gambar berikut, maka luas trapesium BHFE ialah .... m²
9. PATIO/ Ember terbuka di belakang rumah
Nick ingin menciptakan patio terbuka di belakang rumah barunya. Panjang Patio ialah 5, 25 meter dan lebarnya 3 meter. Ia memerlukan 81 buah kerikil bata per m².
Hitunglah berapa banyak kerikil bata yang diharapkan Nick untuk menciptakan pationya itu!
5,5 x 3 x 81 = 1.336,5
10. Perhatikan gambar sebuah jajargenjang berikut
Pada kotak jawaban, buatlah minimal 4 segiempat lain yang berbeda dan mempunyai luas yang sama dengan luas jajargenjang yang ditunjukkan pada gambar di atas. (Catatan: Dua segiempat atau lebih disebut sama bila segiempat yang satu merupakan hasil pencerminan atau perputaran bangkit yang lain)
Pada gambar tersebut ditunjukkan beberapa kemungkinan segiempat yang mempunyai luas yang sama dengan luas jajargenjang pada soal, yaitu 4 satuan luas.
Persegipanjang ialah segi empat yang mempunyai dua pasang sisi sejajar dan sama panjang. Jika L ialah luas, K ialah keliling, p ialah panjang, dan l ialah lebar sebuah persegi panjang, maka: L = p × l dan K = 2p + 2l.
Persegi ialah persegipanjang yang semua sisinya sama panjang. Jika L ialah luas, K ialah keliling, r ialah sisi sebuah persegi, maka: L = r × r dan K = 4 × r.
Trapesium ialah segi empat yang mempunyai sempurna satu pasang sisi sejajar. Jika L ialah luas, K ialah keliling, b ialah panjang alas, a ialah sisi atas, t ialah tinggi sebuah trapesium, maka: L = a + b/2 ×t dan. K = jumlah seluruh panjang sisinya.
Jajargenjang ialah segiempat yang mempunyai dua pasang sisi sejajar dan sudut-sudut yang berhadapan sama besar. Misalkan L ialah luas, K ialah keliling, a ialah panjang alas, l ialah lebar, dan t ialah tinggi sebuah jajargenjang, maka: L = a x t.
Belahketupat ialah segiempat yang mempunyai dua pasang sisi sejajar dan kedua diagonal bidangnya saling tegak lurus. Sebuah belahketupat dengan panjang sisinya a dan panjang diagonal bidangnya d1 dan d2 maka luas dan kelilingnya berturut-turut adalah: L = 1/2 x d1 + d2 dan K = 4 × a.
Layang-layang ialah segiempat yang mempunyai dua pasang sisi yang sama panjang dan dua diagonal bidang yang saling tegak lurus. Sebuah layang-layang dengan panjang sisi s1 dan s2, serta panjang diagonalnya masing-masing d1 dan d2, maka luas dan kelilingnya berturut-turut adalah: L = 1/2 x d1 × d2 dan K = 2s1 + 2s2.
Terdapat beberapa jenis segitiga, yaitu: samasisi, segitiga samakaki, segitiga sebarang, segitiga siku-siku, segitiga tumpul, segitiga lancip. Jika L ialah luas, K ialah keliling, t ialah tinggi, a ialah bantalan sebuah segitiga, dan ketiga sisinya ialah p, q,dan r, maka: L = 1/2 (a × t) dan K = p + q + r.
A. Soal Pilihan Ganda
1. Jika suatu persegi mempunyai luas 144 cm², maka panjang sisinya sama dengan ... mm
| A. | 1,2 mm | C. | 120 mm |
| B. | 12 mm | D. | 1.200 mm |
Sisinya = √14.400 mm² = 120 mm
2. Aisyah mempunyai sebuah kain yang berbentuk persegipanjang. Ia berencana menghias sekeliling kain tersebut dengan renda. Jika ternyata renda yang diharapkan Aisyah paling sedikit 450 cm, salah
satu ukuran kain yang dimiliki Aisyah ialah ...
| A. | 125 × 100 | C. | 125 × 175 |
| B. | 125 × 150 | D. | 125 × 200 |
450 cm = 2(p+l)
(p+l) = 450/2=225 cm
Perkiraan ukuran kain, ada beberapa kemungkinan,diantaranya
Panjang 125 dan Lebar 100 cm
3. Ukuran diagonal-diagonal suatu layang-layang yang mempunyai luas 640 cm² ialah ....
| A. | 22 × 30 | C. | 30 × 36 |
| B. | 32 × 40 | D. | 32 × 46 |
640 = 1/2 x d₁ x d₂
d₁ x d₂ = 1280
dari sini ukuran d₁ dan d₂ sanggup saja,
40 cm dan 32 cm,
80 cm dan 16 cm,
64 cm dan 20 cm,
4. Perhatikan gambar persegi panjang dan persegi berikut
| A. | 4 cm | C. | 4,5 cm |
| B. | 4,25 cm | D. | 4,75 cm |
Luas persegi = 8,5 x 8,5 =72,25
Apabila 1/2 berarti 72,25 : 0,5 =36,125
Luas persegi panjang = 36,125 : 8,5 = 4,25 cm
Kaprikornus lebar persegi panjang ialah 4,25 cm
5. Banyak persegi pada Gambar berikut ialah ….
| A. | 30 | C. | 45 |
| B. | 40 | D. | 55 |
6. Perhatikan gambar berikut. Bangun yang mempunyai luas terbesar ialah ....
| A. | Gambar (a) | C. | Gambar (c) |
| B. | Gambar (b) | D. | Gambar (a) dan (c) |
7. Perhatikan gambar berikut.
Keliling bangkit pada gambar di atas ialah ....
| A. | 40 cm | C. | 20 cm |
| B. | 26 cm | D. | 16 cm |
8. Luas kawasan pada gambar di bawah ialah …..
| A. | 16 cm² | C. | 34 cm² |
| B. | 24 cm² | D. | 48 cm² |
9. Perhatikan gambar persegi ABCD dan persegi KLMN.
| A. | 16 cm² | C. | 32 cm² |
| B. | 25 cm² | D. | 32 cm² |
10. Perhatikan gambar berikut.
| A. | 40 cm² | C. | 140 cm² |
| B. | 120 cm² | D. | 160 cm² |
L persegi panjang = p x l = 12 x 5 = 60 cm²
→ Luas kawasan tidak diarsir = (luas persegi + persegi panjang) - luas arsir
→ L total = (160 - 20) cm²
→ L = 140 cm²
11. Nilai panjang FB dari jajargenjang berikut ialah …
| A. | 5,4 cm | C. | 8 cm |
| B. | 7,2 cm | D. | 9 cm |
12. Perhatikan gambar berikut.
| A. | 120 cm² | C. | 80 cm² |
| B. | 96 cm² | D. | 40 cm² |
13. Berdasarkan gambar berikut, nilai x ialah ....
| A. | 70° | C. | 80° |
| B. | 67° | D. | 100° |
14. Perhatikan gambar belahketupat ABCD.salah
| A. | 60° | C. | 120° |
| B. | 90° | D. | 150° |
15. Perhatikan gambar di samping
| A. | 3 cm | C. | 9 cm |
| B. | 6 cm | D. | 10 cm |
16. Perhatikan lukisan berikut.
| A. | 4, 1, 2, 3 | C. | 3, 1, 4, 2 |
| B. | l, 3, 2, 4 | D. | 3, 2, 1, 4 |
Cara melukis garis bagi
- Lukislah busur bulat yang berpusat di titik M sampai memotong sisi KM dan KL (busur 3). Tandai kedua titik potong tersebut masing-masing dengan titik P dan Q.
- Dari titik P dan Q, lukislah busur bulat sampai berpotongan di dalam segitiga (busur 1 dan 2). Tandai titik potong tersebut dengan titik R.
- Tarik garis dari titik M ke titik R sampai mengenai sisi KL (garis 4). Garis inilah yang disebut garis bagi.
Jadi, urutan cara melukis garis bagi pada segitiga tersebut ialah 3, 1, 2, 4 atau 3, 2, 1, 4 (D).
17. Gambar di bawah ini,
EFGH ialah ....
| A. | 2 m | C. | 6 m |
| B. | 4 m | D. | 8 m |
18. Jika luas satu persegi kecil ialah 4 m², maka luas bangkit datar pada gambar di bawah ialah ...
| A. | 36 cm² | C. | 144 cm² |
| B. | 96 cm² | D. | 162 cm² |
19. Perhatikan gambar berikut.
| A. | 24 cm² | C. | 78 cm² |
| B. | 44 cm² | D. | 72 cm² |
20. Suatu kardus polos dari kertas berbentuk kubus. Volume kardus ialah 64.000 cm³. Fitri memotong sempurna pada rusuk kubus dan mengambil dua sisi bab samping kardus tersebut. Fitri menciptakan garis pada satu potong sisi kardus dan diperolah satu segitiga siku-siku yang perbandingan dua sisi siku-siku ialah 1 : 2. Pada satu potongan sisi kardus yang lain dilukis satu segitiga sama kaki (lihat gambar). Jika ternyata dua segitiga ini sama luasnya, maka panjang sisi yang sama pada segitiga sama kaki ialah .... cm
| A. | 10 | C. | 20 |
| B. | 10 √2 | D. | 20 √2 |
A. Soal Uraian
1. Misalkan suatu persegi diletakkan berimpit di kanan persegi yang lainnya. Tentukan keliling persegi yang terdiri dari:
b. Gabungan 2 persegi. 6s
c. Gabungan 3 persegi. 8 s
d. Gabungan n persegi. (2n + 2)s
e. Berikan alasan yang dipakai untuk menggeneralisasi soal butir d.
Dengan memperhatikan referensi mulai keliling 1 persegi, 2 persegi, 3 persegi, dan seterusnya. Membentuk referensi bilangan genap yang dimulai dari bilangan 4, sehingga didapat untuk sebanyak n persegi = (2n + 2)s
2. Misalkan a merupakan bantalan jajar genjang PQRS dengan t merupakan tingginya. Jika 2t = 3a, tentukan:
b. panjang bantalan dan tingginya bila luas jajar genjang tersebut 864 cm².
L = a x t
864 = a x (3/2)a
864 = (3/2) a²
a² = 864 x 2/3
a² = 576
a = 24 Cm
t = (3/2)t
t = (3/2) x 24
t = 36
3. Diketahui keliling ΔKLM ialah 40 cm.
b. Tentukan panjang sisi ΔKLM !
KL = LM = 2x - 5 , KM = x
keliling = KL + LM + KM
=> (2x - 5) + (2x - 5) + x = 40
=> 5x - 10 = 40
=> 5x = 50
=> x = 10
KL = LM = 2x -5 = 2.10 - 5 = 15
KM = 10
4. Keliling segi-4 PQRS pada gambar di bawah ialah 22 cm.
b. Bagaimanakah caramu menghitung luas PQRS?
c. Berapakah luas PQRS? L=5,5 x 5,5 = 30,25 cm²
5. Diketahui bangun-bangun menyerupai berikut.
b. Bangun manakah yang mempunyai luas terbesar? Bangun (a)
6. Perhatikan gambar berikut.
Gunakan Teorema Pythagoras untuk memilih panjang AC. Perhatikan AP, PC, DP, dan PB. Kemudian perhatikan persegi kecil yang berada didalam persegi ABCD! Yaitu Terdiri dari 9 persegi kecil, sehingga garis AD membagi menjadi 3 bab yang sama besar, begitu juga panjang diagonal-diagonalnya membagi menjadi 3 bab yang sama besar,
Dapatkan Luas kawasan EDFGH = Luas persegi ABCD – 2Luas BCE – Luas ΔBHG.
Jadi, Luas kawasan EDFGH = 4/3 cm²
7. Perhatikan gambar di bawah.
Carilah panjang p + q, luas persegi besar, luas segitiga ABC Dapatkan, Luas kawasan yang diarsir = Luas persegi – 8 Luas segitiga ABC Jadi, luas kawasan yang diarsir ialah 8 cm²
8. Diketahui luas persegi ABCD ialah 25 m2. Jika E, F, dan G masing-masing ialah titik tengah AB, AD, dan CD menyerupai pada gambar berikut, maka luas trapesium BHFE ialah .... m²
Nick ingin menciptakan patio terbuka di belakang rumah barunya. Panjang Patio ialah 5, 25 meter dan lebarnya 3 meter. Ia memerlukan 81 buah kerikil bata per m².
5,5 x 3 x 81 = 1.336,5
10. Perhatikan gambar sebuah jajargenjang berikut
Pada gambar tersebut ditunjukkan beberapa kemungkinan segiempat yang mempunyai luas yang sama dengan luas jajargenjang pada soal, yaitu 4 satuan luas.