Keliling Dan Luas Segitiga
Monday, March 23, 2020
Edit
Segitiga yaitu berdiri datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik sudut. Di sekitar kita, terdapat banyak sekali objek, menyerupai gedung yang bentuk permukaan bangunannya merupakan tempat segitiga. Demikian juga kita sanggup cermati bahtera layar dan bahtera yang dipakai nelayan menangkap ikan. Berbagai permasalahan kehidupan banyak yang sanggup dipecahkan menerapkan banyak sekali konsep dan aturan-aturan pada segitiga.
Ketika mempelajari luas dan keliling segitiga nantinya akan memakai dalil phytagoras. Dalil Pythagoras hanya berlaku pada segitiga siku-siku. Pythagoras menyatakan bahwa: c² = a² + b². Jika ada tiga buah bilangan a, b dan c yang memenuhi persamaan di atas, maka ketiga bilangan tersebut disebut sebagai Triple Pythagoras.
Secara umum untuk menemukan luas dan keliling memakai rumus Luas = 1/2 x a x t dan keliling = sisi a + sisi b + sisi c. Selanjutna mari kita pelajari luas dan keliling segitiga lebih lanjut.
Ayo Kita Menalar
Contoh :
Hitunglah luas tempat berdiri berikut.
Ayo Kita Mencoba
Buatlah ilustrasi materi kain yang dipakai bahtera layar dalam bentuk persegi dengan ukuran 10 cm Berilah tanda pada titik-titik sudut persegi, misalkan ABCD. Kemudian berilah tanda titik pada ilustrasi gambar kayu penyangga, misal EF yakni sebagai berikut.
Tentukan luas permukaan layar perahu.
Kemudian tentukan luas kain yang tersedia! Selanjutnya buatlah ilustrasi permukaan kain dengan permukaan layar perahu, sebagai berikut:
Perhatikan kembali gambar permukaan kain ABCD di atas, ada 5 (lima) segitiga yang terbentuk di dalamnya, yaitu segitiga ABE, ADE, BCE, AFE, dan segitiga BEF.
Ayo Kita Berlatih
Kerjakan soal-soal berikut.
1. Tentukan keliling segitiga dibawah ini
2. Perhatikan gambar berikut.
Luas ΔABC pada gambar di atas yaitu 96 cm²
3. Luas sebuah segitiga 84 cm² dan panjang alasnya 12 cm. Tinggi segitiga tersebut yaitu ...
4. Perbandingan bantalan dan tinggi sebuah segitiga yaitu 5 : 4. Jika luas segitiga tersebut 160 cm², maka tingginya yaitu ...
5. Sebuah taman berbentuk persegi panjang dengan ukuran panjang 25 m dan lebar 20 m. Didalam taman terdapat pot bunga yang berbentuk 2 segitiga siku-siku yang kongruen dengan ukuran panjang sisi siku-sikunya 8 m dan 6 m. dan sisanya ditanami rumput. Hitunglah luas tanaman rumput tersebut?
6. Suci mempunyai satu lembar karton bermotif berbentuk persegi dengan panjang sisinya 25 cm. Suci akan menciptakan mainan yang berbentuk menyerupai pada gambar di bawah. Berapakah luas karton yang tidak terpakai?
7. Hitunglah luas berdiri PQRS pada gambar di bawah!
8. Perhatikan tempat segitiga I dan II. Bandingkan luas I dan luas II. Jelaskan.
9. Perhatikan gambar di samping Jika panjang AB = 16 cm, maka luas berdiri ABCDE yaitu ....
10. Pada segitiga ABC yang tumpul di C, titik M yaitu titik tengah AB. Melalui C dibentuk garis tegak lurus pada BC yang memotong AB di titik E. Dari M, ditarik garis memotong BC yang tegak lurus di D. kalau luas segitiga ABC yaitu 54 satuan luas. Maka luas segitiga BED adalah...
BED = 1/2 ABC
BED = 1/2 x 54
BED = 27 satuan luas
11. Diketahui ΔABC dengan panjang sisi AB = AC = BC = 10 cm. melalui titik tengah tiap-tiap sisi AC, AB, dan BC dibentuk titik A₁, B₁, dan C₁ sehingga terbentuk Δ A₁ B₁ C₁ demikian seterusnya. tentukan jumlah semua panjang sisi yang terbentuk dan keliling yang terbentuk.
12. Diketahui ΔABC yaitu segitiga sama kaki dengan AB = BC dan BC = 30 cm. Persegi EFGH mempunyai panjang sisi 12 cm di dalam ΔABC. Berapakah luas ΔAEF ?
Segitiga AEF
Alas = AE = (30 - 12) / 2 = 18 / 2 = 9 cm
tinggi = sisi EF = 12 cm
Luas = 1/2 x 12 x 9 = 54 cm²
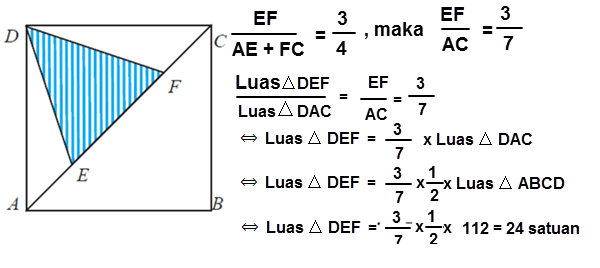
13. Luas persegi panjang ABCD yaitu 112 satuan luas. Titik E dan F berada di diagonal AC menyerupai pada gambar di berikut ini sedemikian sehingga 3(AE + FC) = 4 EF. Luas segitiga DEF adalah… satuan luas
14. Pada ΔABC terdapat titik D pada BC sehingga D : DC = 1 : 3. Titik L pada AD sehingga AL : LD = 1 : 4. Perbandingan luas ΔACL dan ΔBDL yaitu …
15. Perhatikan gambar berikut.
Ada berapa banyak segitiga Gambar (a) yang diharapkan untuk persisi menutupi permukaan persegi panjang Gambar (b).
Ada sebanyak 8 segitiga
Ketika mempelajari luas dan keliling segitiga nantinya akan memakai dalil phytagoras. Dalil Pythagoras hanya berlaku pada segitiga siku-siku. Pythagoras menyatakan bahwa: c² = a² + b². Jika ada tiga buah bilangan a, b dan c yang memenuhi persamaan di atas, maka ketiga bilangan tersebut disebut sebagai Triple Pythagoras.
Secara umum untuk menemukan luas dan keliling memakai rumus Luas = 1/2 x a x t dan keliling = sisi a + sisi b + sisi c. Selanjutna mari kita pelajari luas dan keliling segitiga lebih lanjut.
Ayo Kita Menalar
| No | Nama Bangun | Sifat-sifat |
|---|---|---|
| 1. | Segitiga | Jika a, t dan c merupakan alas, tinggi, dan sisi miring segitiga, maka :
|
| 2. | Hubungan antara persegi dengan segitiga, persegipanjang dengan segitiga, dan jajargenjang dengan segitiga. Keliling segitiga yang terbentuk dari persegi, persegi panjang, dan jajargenjang tidak mempunyai kekerabatan yang pasti, alasannya yaitu keliling segitiganya tetap didapat dari penjumlahan dari ketiga sisi. Luas segitiga didapat dari setengah luas persegi atau persegipanjang ata jajargenjang. | |
| 3. | Luas segitiga tidak selalu setengah dari luas persegipanjang, tergantung pada konteks yang ada. | |
Contoh :
Hitunglah luas tempat berdiri berikut.
| Soal (1) | Soal (2) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Luas segitiga I:
Luas Segitiga II
Sehingga, luas berdiri seluruhnya = L₁ + L₂ = 41 dm² | Bangun tersebut terdiri dari tiga segitiga
|
Ayo Kita Mencoba
Buatlah ilustrasi materi kain yang dipakai bahtera layar dalam bentuk persegi dengan ukuran 10 cm Berilah tanda pada titik-titik sudut persegi, misalkan ABCD. Kemudian berilah tanda titik pada ilustrasi gambar kayu penyangga, misal EF yakni sebagai berikut.
Tentukan luas permukaan layar perahu.
| L = | 1 | × 10 × 10 = 50 |
| 2 |
Perhatikan kembali gambar permukaan kain ABCD di atas, ada 5 (lima) segitiga yang terbentuk di dalamnya, yaitu segitiga ABE, ADE, BCE, AFE, dan segitiga BEF.
Ayo Kita Berlatih
Kerjakan soal-soal berikut.
1. Tentukan keliling segitiga dibawah ini
2. Perhatikan gambar berikut.
Luas ΔABC pada gambar di atas yaitu 96 cm²
3. Luas sebuah segitiga 84 cm² dan panjang alasnya 12 cm. Tinggi segitiga tersebut yaitu ...
4. Perbandingan bantalan dan tinggi sebuah segitiga yaitu 5 : 4. Jika luas segitiga tersebut 160 cm², maka tingginya yaitu ...
5. Sebuah taman berbentuk persegi panjang dengan ukuran panjang 25 m dan lebar 20 m. Didalam taman terdapat pot bunga yang berbentuk 2 segitiga siku-siku yang kongruen dengan ukuran panjang sisi siku-sikunya 8 m dan 6 m. dan sisanya ditanami rumput. Hitunglah luas tanaman rumput tersebut?
6. Suci mempunyai satu lembar karton bermotif berbentuk persegi dengan panjang sisinya 25 cm. Suci akan menciptakan mainan yang berbentuk menyerupai pada gambar di bawah. Berapakah luas karton yang tidak terpakai?
7. Hitunglah luas berdiri PQRS pada gambar di bawah!
8. Perhatikan tempat segitiga I dan II. Bandingkan luas I dan luas II. Jelaskan.
9. Perhatikan gambar di samping Jika panjang AB = 16 cm, maka luas berdiri ABCDE yaitu ....
10. Pada segitiga ABC yang tumpul di C, titik M yaitu titik tengah AB. Melalui C dibentuk garis tegak lurus pada BC yang memotong AB di titik E. Dari M, ditarik garis memotong BC yang tegak lurus di D. kalau luas segitiga ABC yaitu 54 satuan luas. Maka luas segitiga BED adalah...
BED = 1/2 ABC
BED = 1/2 x 54
BED = 27 satuan luas
11. Diketahui ΔABC dengan panjang sisi AB = AC = BC = 10 cm. melalui titik tengah tiap-tiap sisi AC, AB, dan BC dibentuk titik A₁, B₁, dan C₁ sehingga terbentuk Δ A₁ B₁ C₁ demikian seterusnya. tentukan jumlah semua panjang sisi yang terbentuk dan keliling yang terbentuk.
12. Diketahui ΔABC yaitu segitiga sama kaki dengan AB = BC dan BC = 30 cm. Persegi EFGH mempunyai panjang sisi 12 cm di dalam ΔABC. Berapakah luas ΔAEF ?
Segitiga AEF
Alas = AE = (30 - 12) / 2 = 18 / 2 = 9 cm
tinggi = sisi EF = 12 cm
Luas = 1/2 x 12 x 9 = 54 cm²
13. Luas persegi panjang ABCD yaitu 112 satuan luas. Titik E dan F berada di diagonal AC menyerupai pada gambar di berikut ini sedemikian sehingga 3(AE + FC) = 4 EF. Luas segitiga DEF adalah… satuan luas
14. Pada ΔABC terdapat titik D pada BC sehingga D : DC = 1 : 3. Titik L pada AD sehingga AL : LD = 1 : 4. Perbandingan luas ΔACL dan ΔBDL yaitu …
15. Perhatikan gambar berikut.
Ada berapa banyak segitiga Gambar (a) yang diharapkan untuk persisi menutupi permukaan persegi panjang Gambar (b).
Ada sebanyak 8 segitiga