Pintar Pelajaran Rumus Pola Soal Suku Banyak Matematika, Materi, Teorema Faktor Dan Sisa, Persamaan, Nilai, Pembagian Biasa, Bentuk Umum, Horner, Substitusi
Friday, October 25, 2019
Edit
Rumus Contoh Soal Suku Banyak Matematika, Materi, Teorema Faktor dan Sisa, Persamaan, Nilai, Pembagian Biasa, Bentuk Umum, Horner, Substitusi - Anda telah mempelajari fungsi aljabar di SMP, contohnya fungsi y = x2 – 1. Fungsi y = x2 – 1 merupakan fungsi suku banyak. Pada potongan ini konsep, tersebut akan dikembangkan sehingga Anda akan mempelajari bagaimana menjabarkan suku banyak menjadi perkalian beberapa suku banyak. Cara menjabarkan suku banyak tersebut akan Anda pelajari pada potongan ini. Salah satu manfaat mempelajari potongan ini untuk menuntaskan duduk perkara berikut. Hubungan antara jarak yang ditempuh x(t) dan waktu yang diharapkan (t) untuk gerak sebuah kendaraan beroda empat dinyatakan oleh x(t) = 48t2 – 3t. Dalam hal ini, x(t) dalam meter dan t dalam menit. Dengan memakai konsep suku banyak, Anda sanggup menghitung jarak kendaraan beroda empat sesudah bergerak 5 menit.
1. Pengertian Suku Banyak
1.1. Suku Banyak, Derajat Suku Banyak, Koefisien Suku Banyak, dan Suku Tetap
Anda telah memahami bahwa grafik y = (x + 2)2 diperoleh dengan cara menggeser grafik y = x2 sejauh 2 satuan ke kiri, ibarat diperlihatkan pada Gambar 1.
 |
| Gambar 1. Grafik y = (x + 2)2 diperoleh dengan cara menggeser grafik y = x2 sejauh 2 satuan ke kiri. |
Adapun grafik y = (x – 1)3 diperoleh dari grafik y = x3 dengan cara menggeser grafik dari y = x3 sejauh 1 satuan ke kanan ibarat diperlihatkan pada Gambar 2.
Amati keempat persamaan berikut.
 |
| Gambar 2. Grafik y = (x – 1)3 diperoleh dari grafik y = x3 dengan cara menggeser grafik dari y = x3 sejauh 1 satuan ke kanan. |
y = x2
y = (x + 2)2 = x2 + 4x + 4
y = x3
y = (x – 1)3 = x3 – 3x2 + 3x – 1 Ruas kanan keempat persamaan itu merupakan suku banyak dalam peubah (variabel) x. Suku banyak x3 – 3x2 + 3x – 1 terdiri atas empat suku, yaitu suku ke-1 adalah x3, suku ke-2 yaitu –3x2, suku ke-3 yaitu 3x, dan suku ke-4 yaitu –1.
Derajat suatu suku banyak ditentukan oleh pangkat tertinggi dari variabel pada suku banyak tersebut. Jadi, derajat dari suku banyak x3 – 3x2 + 3x – 1 yaitu 3. Koefisien suku banyak dari x3, x2, dan x berturut-turut yaitu 1, –3, dan 3.
Adapun –1 dinamakan suku tetap (konstanta).
Dari uraian tersebut, dapatkah Anda menyatakan suku banyak berderajat n? Cobalah nyatakan suku banyak derajat n secara umum. Secara umum, suku banyak dalam peubah x berderajat n ditulis sebagai berikut.
P(x) = anxn + an–1 xn–1 + an–2 xn–2 +… + a2 x2 + a1x + a0
Cara penyusunan suku banyak menurut pangkat x yang berkurang dengan an, an–1 , … , a1 adalah koefisien-koefisien suku banyak yang merupakan konstanta real dan an ≠ 0.
a0 = suku tetap yang merupakan konstanta real
n = derajat suku banyak dan n yaitu bilanga cacah
1.2. Penjumlahan, Pengurangan, dan Perkalian Suku Banyak
Diketahui, f(x) = –3x3 – x2 + 2x dan g(x) = x8 + 2x5 – 15x2 + 6x + 4
• Penjumlahan suku banyak f(x) dengan g(x) yaitu :
f(x) + g(x)= (–3x3 – x2 + 2x) + (x8 + 2x5 – 15x2 + 6x + 4) = x8 + 2x5 – 3x3 – 16x2 + 8x + 4
• Pengurangan suku banyak f(x) dengan suku banyak g(x) yaitu :
f(x) – g(x) = f(x) + (–g(x))
= (–3x3 – x2 + 2x) + (–x8 – 2x5 + 15x2 – 6x – 4)
= –x8 – 2x5 – 3x3 + 14x2 – 4x – 4 • Perkalian suku banyak f(x) dengan suku banyak g(x) yaitu :
f(x) × g(x) = (–3x3 – x2 + 2x) (x8 + 2x5 – 15x2 + 6x + 4)
= –3x11 – 6x8 + 45x5 – 18x4 – 12x3 – x10 – 2x7 + 15x4 – 6x3 – 4x2 + 2x9 + 4x6 – 30x3 + 12x2 + 8x
= –3x11 – x10 + 2x9 – 6x8 – 2x7 + 4x6 + 45x5 – 3x4 – 48x3 Cobalah Anda tentukan g (x) – f(x) dan g(x) × f(x).
Apakah f(x) – g(x) = g(x) – f(x)?
Apakah f(x) × g(x) = g(x) × f(x)?
Jelaskan dengan kata-kata Anda sendiri, kemudian bacakan di depan kelas.
Ingatlah :
Misalkan, f(x) suku banyak berderajat m dan g(x) suku banyak berderajat n,
- f(x) + g(x) yaitu suku banyak yang derajatnya yaitu maksimum m atau n.
- f(x) – g(x) = f(x) + (–g(x)) yaitu suku banyak berderajat maksimum m atau n.
- f(x) × g(x) yaitu suku banyak berderajat sempurna sama dengan (m + n).
Contoh Soal Suku Banyak 1
Diketahui suku banyak f(x) dan g(x) sebagai berikut.
f(x) = 2x4 – 3x2 + 5x – 6
g(x) = 2x2 – 7x + 10 Tentukan :
a. f(x) + g(x)
b. f(x) – g(x)
c. f(x) × g(x)
Pembahasan 1
a. f(x) + g(x) = (2x4 – 3x2 + 5x – 6) + (2x2 – 7x + 10)
= 2x4 – x2 – 2x + 4
b. f(x) – g(x) = (2x4 – 3x2 + 5x – 6) – (2x2 – 7x + 10)
= 2x4 – 5x2 + 12x – 16
c. f(x) × g(x) = (2x4 – 3x2 + 5x – 6) – (2x2 – 7x + 10)
= 2x4 (2x2 – 7x + 10) – 3x2 (2x2 – 7x + 10) + 5x (2x2 – 7x + 10) – 6 (2x2 – 7x + 10)
= 4x6 – 14x5 + 20x4 – 6x4 + 21x3 – 30x2 + 10x3 – 35x2 + 50x – 12x2 + 42x – 60
= 4x6 – 14x5 + 14x4 + 31x3 – 77x2 + 92x – 602. Cara Menentukan Nilai Suku Banyak
2.1. Cara Substitusi
Anda sanggup memilih nilai g(x) = sin (1/x) untuk x = (2/π) dan x =  , yaitu :
, yaitu :
g (2/π) = sin = sin (π/2) = 1
= sin (π/2) = 1
g = sin
= sin  = sin π = 1
= sin π = 1
g (2/π) = sin
g
Akan tetapi, Anda akan mengalami kesulitan kalau harus memilih g(π) = sin (1/π) karena (1/π) bukan merupakan sudut istimewa.
Lain halnya dengan fungsi suku banyak, berapa pun nilai yang diberikan pada peubahnya, Anda dengan gampang sanggup memilih nilai suku banyak itu.
Diketahui, suku banyak P(x) = 3x4 – 2x2 + 5x – 6 maka :
• untuk x = 1, diperoleh P(1) = 3(1)4 – 2(1)2 + 5(1) – 6 = 0
• untuk x = –1, diperoleh P(–1) = –10
• untuk x = 0, diperoleh = –6
• untuk x + 2 = 0 atau x = –2, diperoleh P(–2) = 24
• untuk x – 2 = 0 atau x = 2, diperoleh P(2) = 44
Kemudian, misalkan suku banyak P(x) = 5x3 + 4x2 – 3x – 2 maka :
• untuk x = k + 1, diperoleh :
P(k + 1) = 5 (k + 1)3 + 4 (k + 1)2 – 3 (k + 1) – 2
P(k + 1) = 5 k3 + 19 k2 + 20k + 4 • untuk x = k – 1, diperoleh :
P(k – 1) = 5 (k – 1)3 + 4 (k – 1)2 – 3 (k – 1) – 2 = 5k3 – 11k2 + 4k
• untuk x = –k
P(–k) = –5k3 + 4k2 + 3k – 2
• untuk x = –k + 1, diperoleh :
P(–k + 1) = –5k3 + 19k2 – 20k + 4
Dari uraian tersebut, dapatkah Anda menduga rumus memilih nilai suku banyak? Cobalah nyatakan rumus tersebut dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut memperjelas ketentuan berikut.
Nilai suku banyak :
P(x) = anxn + an–1xn–1 + an–2xn–2 + ...+ a2x2 + a1x + a0, untuk x = k di mana k suatu bilangan real yaitu :
2.2. Cara Skema
Untuk memilih nilai dari suatu suku banyak dengan nilai tertentu bagi peubahnya akan lebih gampang kalau Anda memakai cara skema dibandingkan dengan cara substitusi. Agar lebih jelas, pelajari uraian berikut.
Diketahui :
P(x) = 3x4 + 2x2 – 5x + 6
P(x) = 3x4 + 2x2 – 5x + 6
P(x) sanggup pula disusun sebagai berikut.
P(x) = 3x4 + 2x2 – 5x + 6
= 3x4 + 0x3 + 2x2 – 5x + 6
= (3x3 + 0x2 + 2x – 5) x + 6
= [(3x2 + 0x + 2) x – 5] x + 6
= [[(3x + 0 )x + 2] x – 5] x + 6 …(1) Jika nilai x = 2 disubstitusikan pada persamaan (1) maka :
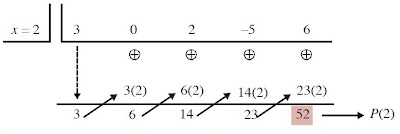
P(2) secara sedikit demi sedikit diperoleh sebagai berikut.
P(x) = [[(3x + 0)x + 2] x – 5]x + 6
P(2) = [[(3.2 + 0)2 + 2]2 – 5]2 + 6 = [(6.2 + 2)2 – 5]2 + 6
P(2) = (14.2 – 5) 2 + 6 = 23.2 + 6 = 52 Mari menganalisis proses pada perhitungan tersebut.
• Langkah ke-1 menghitung (3.2) + 0 = 6
• Langkah ke-2 menghitung (6.2) + 2 = 14
• Langkah ke-3 menghitung (14.2) – 5 = 23
• Langkah ke-4 menghitung (23.2) + 6 = 52
Langkah-langkah itu sanggup disajikan dalam skema (skema) sebagai berikut.
Perhitungan untuk memperoleh P(2) sanggup disajikan melalui skema berikut. Namun, amatilah bahwa ada dua operasi dalam proses ini, yaitu perkalian dan penjumlahan.
• Nilai x = 2 dituliskan pada baris pertama skema, kemudian diikuti oleh koefisien setiap suku dari pangkat tertinggi ke terendah dan suku tetap.
• Operasi aljabar pada skema tersebut yaitu perkalian dan penjumlahan.
Secara umum, perhitungan nilai suku banyak :
P(x) = anxn + an–1xn-1 + an–2xn–2 + .... + a2x2 + a1x + a0
untuk x = k memakai cara skema, diperlihatkan pada Gambar 3.
dengan:
An = an
An – 1 = An(k) + an – 1
An – 2 = An–1(k) + an – 2 . .
. .
. .
A2 = A3(k) + a2
A1 = A2(k) + a1
A0 = A1(k) + a0 |
| Gambar 3. Skema proses perhitungan P(k). |
Contoh Soal Suku Banyak 2
a. Hitunglah nilai f(x) = 2x4 – 4x3 + 4x – 2 untuk x = –6 memakai cara skema.
b. Suku banyak f(x) = 2x5 – 3x4 + 2x3 – px + 10, untuk x = 2 yaitu f(2) = 38. Berapakah nilai p?
f(2) = 38
f(2) = 42 – 2p
↔ 38 = 42 – 2p
↔ 2p = 4
↔ p = 2
3. Pembagian Suku Banyak
3.1. Pengertian Pembagi, Hasil Bagi, dan Sisa Pembagian
Masih ingatkah Anda dengan pembagian bersusun pada bilangan bulat? Jika ya, coba tentukan pembagian 156 oleh 8. Proses pembagian suku banyak pun memiliki proses yang hampir sama dengan pembagian bilangan bulat. Untuk mengetahui hasil bagi dan sisa pembagian suku banyak, Anda perlu menguraikan suku banyak menjadi perkalian beberapa suku banyak. Agar lebih jelasnya, pelajari uraian berikut.
Amati perkalian-perkalian berikut.
a. (x + 1)(x + 2)(2x – 3) = (x2 + 3x + 2)(2x – 3) = 2x3 + 3x2 – 5x – 6
b. (x – 1)(x3 – 3) = x4 – x3 – 3x + 3 Amatilah proses perkalian tersebut dengan saksama. Dari perkalian (x + 1)(x + 2)(2x – 3), dihasilkan suatu suku banyak 2x3 + 3x2 – 5x – 6. Dengan kata lain, kalau diberikan atau diketahui suatu suku banyak, dapatlah suku banyak itu difaktorkan. Dengan demikian, Anda sanggup lebih gampang melaksanakan pembagian terhadap suatu suku banyak.
Diketahui, P(x) = x3 – 7x2 + 4x + 50 yaitu suku banyak berderajat 3.
Coba Anda jelaskan langkah-langkah yang dilakukan dalam pembagian tersebut. (x – 3) yaitu pembagi dari P(x), sedangkan hasil bagi dari P(x) adalah x2 – 4x – 8 dan sisa pembagiannya yaitu 26.
Jadi, (x3 – 7x2 + 4x + 50) : (x – 3) = x2 – 4x – 8 dengan sisa 26. Akibatnya, suku banyak P(x) sanggup ditulis sebagai x3 – 7x2 + 4x + 50 = (x – 3 ) (x2 – 4x – 8) + 26 atau P(x) = (x – 3) × H(x) + sisa … (i),
dengan H(x) = x2 – 4x – 8 dan sisa = 26.
Jika nilai x = 3 disubstitusikan pada persamaan (i), diperoleh :
P(3) = (3 – 3 ) × H(3) + sisa = 0 × H(3) + sisa = sisa
Jadi, sisa pembagian oleh (x – 3) terhadap P(x) yaitu P(3).
Dari uraian tersebut, dapatkah Anda menduga bentuk umum pembagian suku banyak? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep pembagian suku banyak yang telah Anda pelajari tersebut memperjelas ketentuan berikut.
Sisa pembagian oleh (x – k) terhadap P(x) = anxn + an–1xn–1 + an–2xn–2 + .... + a2x2 + a1x + a0 adalah P(k) atau P(x) = (x – k) H(x) + sisa dengan sisa = P(k).
Informasi untuk Anda :
Ada beberapa lambang yang dipakai untuk pembagian. Lambang yang paling umum dipakai yaitu ibarat tanda kurung dengan garis horizontal pada potongan atasnya ( )─ ). Tanda kurung diperkenalkan pada awal tahun 1500. Beberapa waktu kemudian, tanda garis horizontal ditambahkan. Adapun lambang “ : “ (disebut obelus) kali pertama dipakai sebagai pembagi sekitar tahun 1650. Lambang tersebut diperkenalkan oleh Matematikawan Inggris, John Pell.
Ada beberapa lambang yang dipakai untuk pembagian. Lambang yang paling umum dipakai yaitu ibarat tanda kurung dengan garis horizontal pada potongan atasnya ( )─ ). Tanda kurung diperkenalkan pada awal tahun 1500. Beberapa waktu kemudian, tanda garis horizontal ditambahkan. Adapun lambang “ : “ (disebut obelus) kali pertama dipakai sebagai pembagi sekitar tahun 1650. Lambang tersebut diperkenalkan oleh Matematikawan Inggris, John Pell.
Contoh Soal 3
Tentukan sisa pembagian untuk suku banyak (3x4 + 2x2 + 5x – 1) : (x – 1)
Jawaban :
Sisa = P(1) = 3.14 + 2.12 + 5.1 – 1 = 9.
3.2. Pembagian Suku Banyak dengan Cara Horner
3.2.1. Pembagian Suku Banyak dengan (x – k)
Anda telah mengetahui P(x) = anxn + an – 1xn – 1 + an – 2 xn – 2 + … + a2 x2 + a1x + a0 dibagi (x – k) hasil baginya yaitu H(x) dan sisanya P(k). Secara matematis, ditulis P(x) = (x – k)H(x) + sisa, dengan sisa = A0 = P(k).
Diketahui P(x) = a3x3 + a2 x2 + a1x + a0 dan (x – k) yaitu pembagi P(x). Oleh alasannya yaitu P(x) berderajat 3 dan (x – k) berderajat 1 maka derajat H(x) yaitu (3 – 1) = 2 dan derajat sisa yaitu (1 – 1) = 0.
Berdasarkan kesamaan suku banyak tersebut (pada kedua ruas), Anda sanggup memilih nilai b2, b1, b0, dan A0 dengan langkah-langkah sebagai berikut.
• Langkah ke-1: b2 = a3
• Langkah ke-2: b1 – b2k= a2 → b1 = a2 + b2k = a2 + a3k
• Langkah ke-3: b0 – b1k = a1 → b0 = a1 + b1k = a1+ (a2 + a3k)k = a1 + a2k + a3k2
• Langkah ke-4: A0 – b0k = a0 → A0 = a0 + b0k
= a0 + (a1 + a2k + a3k2)k
= a0 + a1k + a2k2 + a3k3.Contoh Soal 4
a. Tentukan hasil bagi dan sisa pembagian dari (4x3 – 10x2 + 14x – 15) : (x –5) menggunakan cara Horner.
b. Jika fungsi suku banyak P(x) = 6x5 + 41x4 + 97x3 + px2 + 41x + 6 habis dibagi dengan (x – 3), tentukan nilai p.
Jadi, hasil bagi dari (4x3 – 10x2 + 14x – 15) oleh (x –5) yaitu 4x2 + 10x + 64 dan sisanya yaitu 305.
b.
P(x) = 6x5 + 41x4 + 97x3 + px2 + 41x + 6 habis dibagi dengan (x – 3) maka sisa pembagiannya sama dengan nol sehingga 7.527 + 9p = 0
P(x) = 6x5 + 41x4 + 97x3 + px2 + 41x + 6 habis dibagi dengan (x – 3) maka sisa pembagiannya sama dengan nol sehingga 7.527 + 9p = 0
↔ 9p = –7.527
↔ p = – 836 (1/3) Ingatlah :
Dari Contoh 4 (a) diperoleh sisa pembagian yaitu nol. Dikatakan suku banyak P(x) habis dibagi oleh ax + b.
3.2.2. Pembagian Suku Banyak dengan (ax + b)
Untuk memilih hasil bagi dan sisa pembagian suku banyak (x3 – 2x2 + 3x – 5) : (2x + 3), terlebih dahulu Anda harus menuliskan bentuk (2x + 3) menjadi 2(x + 3/2).
Dengan demikian,
(x3 – 2x2 + 3x – 5) : (2x + 3) = (x3 – 2x2 + 3x – 5) : 2(x + 3/2)
Pembagian suatu suku banyak oleh (ax + b) dinyatakan sebagai berikut.
Diketahui, k = - (b/a) maka bentuk (x – k) sanggup dinyatakan sebagai :

Pembagian suku banyak P(x) oleh (x + b/a) memperlihatkan korelasi berikut.
P(x) = (x + b/a) H(x) + sisa
= 1/a (ax + b) H(x) + sisa
= (ax + b)  + sisa ....(*)
+ sisa ....(*)
Persamaan (*) merupakan suku banyak P(x) dibagi (ax + b) memperlihatkan hasil bagi H(x) dan sisa pembagian. Nilai sisa dan koefisien-koefisien H(x) ditentukan dengan cara pembagian Horner untuk x = – (b/a).
Ingatlah :
Dari tumpuan tersebut, kalau pembagian suku banyak menghasilkan sisa sama dengan nol, dikatakan P(x) habis dibagi oleh (x – k) dan (x – k) disebut faktor dari P(x).
Contoh Soal 5
Tentukan hasil bagi dan sisa pembagian dari (4x3 – 10x2 + 14x – 15) : (2x – 5) memakai cara Horner.
Jadi, hasil baginya adalah  = 2x2 + 7 dan sisanya adalah 20.
= 2x2 + 7 dan sisanya adalah 20.
3.2.3. Pembagian Suku Banyak dengan ax2 + bx + c, dengan a ≠ 0
Pembagian (x3 – x2 + 4x – 4) oleh (x2 – 1) sanggup dituliskan sebagai berikut:
P(x) = (x2 – 1 ) H(x) + sisa = (x + 1) (x – 1) H(x) + (A1x + A0)
untuk x = 1 diperoleh P(1) = 0 . H(x) + (A0 + A1(1) ) = A1 + A0
untuk x = –1 diperoleh, P(–1) = 0 . H(x) + (A0 + A1(–1)) = – A1 + A0
Dengan demikian, sisa pembagian adalah A0 + A1x, yaitu –5 + 5x.
Coba Anda tentukan pembagian (x3 – x2 + 4x –4) : (x2 – 1) dengan pembagian biasa ibarat pada bilangan bulat. Adapun hasil bagi ditentukan sebagai berikut.
Jadi, H(x) = b1x + b0 = x – 1. Coba amati kembali skema tersebut. Sisa dari pembagian mana angka 5?
Untuk pembagian suku banyak oleh P(x) = ax2 + bx + c, a ≠ 0, di mana P(x) tidak sanggup difaktorkan maka dipakai cara pembagian biasa, ibarat pada bilangan. Adapun untuk P(x) yang sanggup difaktorkan dipakai cara pembagian biasa dan skema Horner.
4. Teorema Sisa
Diketahui, P(x) = anxn + an – 1 xn – 1 + … + a2x2 + a1x + a0
Cara Anda memilih sisa pembagian dari pembagian suku banyak P(x) oleh bentuk (x – k), (ax + b), dan (ax2 + bx + c), baik dengan cara Horner maupun dengan cara pembagian biasa telah dipelajari pada pelajaran sebelumnya.
Sekarang amatilah persamaan berikut:
P(x) = f(x) . H(x) + S
P(x) : suku banyak yang dibagi
f(x) : pembagi
H(x) : hasil bagi
S : sisa pembagian
Jika P(x) berderajat n dan f(x) berderajat m (m ≤ n) maka derajat H(x) dan S masing-masing sebagai berikut.
• derajat H(x) yaitu (n – m)
• derajat maksimum S yaitu (m – 1)
4.1. Pembagian dengan Pembagi (ax + b)
Jika f(x) = ax + b, merupakan pembagi dari P(x) maka korelasi antara P(x) dan f(x) sanggup ditulis sebagai berikut.
P(x) = (ax + b) + S, berlaku untuk setiap x bilangan real.
+ S, berlaku untuk setiap x bilangan real.
Oleh leh alasannya yaitu f(x) berderajat satu maka S berderajat nol.
Jadi, konstanta S sama dengan A0.
Sisa pembagian sanggup ditentukan dengan memakai teorema berikut.
Teorema 1 :
Jika suku banyak P(x) yang berderajat n dibagi dengan (ax + b) maka sisanya yaitu P(- b/a).
Bukti: harus ditunjukkan bahwa S = P (- b/a) Jika suku banyak P(x) berderajat n dibagi dengan (ax + b), bentuk pembagian itu dituliskan sebagai berikut :
P(x) = (ax + b)  + S … (1)
+ S … (1)
Selanjutnya, substitusikan nilai x = - b./a ke persamaan (1) sehingga diperoleh :
Contoh Soal 6
Carilah sisa pembagian dari (4x3 + 2x2 – 4x + 6) : (x – 3) tanpa melaksanakan pembagian terlebih dahulu.
Jawaban 6
Suku banyak P(x) = 4x3 + 2x2 – 4x + 6 dibagi dengan (x – 3) sisanya adalah
S = P (3/1) = P(3) (berdasarkan Teorema 6.1).
Jadi, dengan menyubstitusikan x = 3 ke dalam fungsi P(x), diperoleh :
P(3) = 4.33 + 2.32 – 4.3 + 6 = 120.
Dengan demikian, sisa pembagiannya yaitu 120.
Contoh Soal 7
Tentukanlah p biar pembagian (6x2 + 7x – 5) : (px – 1) menghasilkan sisa pembagian yang bernilai 0.
Kunci Jawaban 7
Suku banyak P(x) = 6x2 + 7x – 5 dibagi dengan (px – 1), sisanya yaitu :
S = P (1/p) (berdasarkan Teorema 1). Jadi, dengan mensubstitusikan x = 1/P ke dalam fungsi P(x), diperoleh :
sehingga sisa pembagian yaitu : 
Sisa pembagian sama dengan nol maka berlaku :
Penyebut dihentikan sama dengan nol sehingga :
–5p2 + 7p + 6 = 0
5p2 – 7p – 6 = 0 Dengan memakai rumus abc diperoleh :
4.2. Pembagian dengan Pembagi (x – a)(x – b)
Suatu suku banyak p(x) yang dibagi oleh f(x) = (x – a) (x – b), sanggup dituliskan sebagai berikut.
P(x) = (x – a) (x – b) H(x) + S … (1)
berlaku untuk setiap x bilangan real.
f(x) = (x – a) (x – b) berderajat 2 sehingga sisanya berderajat maksimum satu, atau S = A0 + A1x.
Coba Anda jelaskan mengapa sisanya berderajat maksimum satu.
Dengan demikian, persamaan (1) sanggup dituliskan sebagai berikut.
P(x) = (x – a) (x – b) . H(x) + A1x + A0
Sisa sanggup ditentukan dengan teorema sisa, yaitu sebagai berikut.
• Untuk pembagi (x – a), diperoleh sisa :
P(a) = 0. H(a) + A1(a) + A0
P(a) = A1a + A0 … (2).
• Untuk pembagi (x – b), diperoleh sisa :
P(b) = 0. H(b) + A1(b) + A0
P(b) = A1b + A0… (3).
Contoh Soal 8 ( Soal Ebtanas 1999)
Suatu suku banyak P(x) dibagi oleh (x2 – 1) sisanya (12x – 23) dan kalau dibagi oleh (x – 2) sisanya 1. Sisa pembagian suku banyak oleh (x2 – 3x + 2) yaitu ....
Jawaban 8
(x2 – 1) = (x + 1)(x – 1)
Jika P(x) dibagi (x – 1), sisanya S = f(1) = 12(1) – 23 = – 11.
Jika P(x) dibagi (x – 2) sisa S = f(2) = 1 (diketahui).
Jika P(x) dibagi (x2 – 3x + 2) = (x – 2)(x – 1) sisanya yaitu :
Contoh Soal 9
Jika suku banyak P(x) dibagi oleh (x – 2), sisanya 8. Adapun kalau P(x) dibagi oleh (x2 – x – 6), sisanya (3x – 6). Berapa sisa pembagian P(x) oleh (x2 – 4)?
Jawaban 9
Pernyataan P(x) dibagi oleh (x – 2) bersisa 8 sanggup ditulis dalam bentuk persamaan P(x) = (x – 2) H(x) + 8 yang berlaku untuk setiap x bilangan real.
Untuk x = 2, diperoleh P(2) = 8.
Pernyataan P(x) dibagi oleh (x2 – x – 6) bersisa (3x – 6) sanggup ditulis dalam persamaan
P(x) = (x – 3) (x + 2) H(x) + 3x – 6 yang berlaku untuk setiap x bilangan real.
• Untuk x = 3, diperoleh P(3) = 3.
• Untuk x = –2, diperoleh P(–2) = –12.
Misalkan, sisa pembagian P(x) oleh x2 – 4 adalah S = A1 x + A0 maka bentuk pembagian sanggup dituliskan dalam persamaan P(x) = (x + 2) (x – 2) H(x) + A1 x + A0 yang berlaku untuk setiap x bilangan real.
• Untuk x = 2, diperoleh P(2) = 2A1 + A0 = 8 ....(*)
• Untuk x = –2, diperoleh P(–2) = –2A1 + A0 = –12 ....(**)
Dari persamaan (*) dan (**) diperoleh A0 = –2 dan A1 = 5 (coba buktikan!)
Jadi, sisa pembagian P(x) oleh (x2 – 4) yaitu S = 5x – 2.
5. Teorema Faktor
5.1. Pengertian Teorema Faktor
Pandanglah suku banyak P(x) dan pembagi ax + b. Kemudian, amati kembali Teorema 5.1 dengan saksama. Jika sisanya 0, apa yang terjadi dengan (ax + b)? Sebagai akhir dari Teorema 5.1, kalau sisa 
P(x) = (ax + b)  + 0
+ 0
↔ P(x) = (ax + b)  dengan a ≠ 0.
dengan a ≠ 0.
Hal ini memperlihatkan bahwa (ax + b) yaitu suatu faktor dari P(x). Dengan demikian, sanggup dikatakan kalau P(x) yaitu suatu polinom, ax + b yaitu pembagi, dan sisa pembagiannya yaitu 0 atau  = 0 maka ax + b adalah faktor dari P(x).
= 0 maka ax + b adalah faktor dari P(x).
Ingatlah :
Selain untuk memilih faktor suatu suku banyak, teorema faktor sanggup pula dipakai untuk memilih koefisien-koefisien suku banyak yang belum diketahui.
Contoh Soal 10
Tentukan nilai k sehingga (x + 3a) merupakan faktor dari x3 + (ak + 2a) x2 + 18a3
Pembahasan 10
Berdasarkan teorema faktor maka :
f(–3a) = 0
(–3a)3 + (ak + 2a) (–3a)2 + 18a3 = 0
–27a3 + (ak + 2a) 9a2 + 18a3 = 0
–27a3 + 9a3k + 18a3 + 18a3 = 0
(–27 + 9k + 36) a3 = 0
(9 + 9k) a3 = 0 atau
9 + 9k = 0
9k = –9
k = –1
Teorema 2 :
Jika P(x) = anxn + an–1 . xn–1 + . . . + a1 . x + a0 dengan ai bilangan bulat, i = 1, 2, ..., n dan p bilangan bundar dengan p merupakan harga nol dari P(x) maka p yaitu pembagi a0.
Bukti :
Misal, p bilangan bundar yang merupakan harga nol P(x) maka :
P(p) = an pn + an–1 . pn–1 + … + a1 p + a0 = 0
an pn + an–1 . pn–1 +… + a1 p = –a0
p(an . pn–1 + an–1 . pn–2 + … + a1) = –a0 Oleh alasannya yaitu p yaitu bilangan bundar dan ai juga yaitu bilangan bundar maka ruas kiri persamaan tersebut merupakan bilangan bulat. Jadi, p pembagi dari a0 (terbukti).
Contoh Soal 11
Tentukanlah faktor-faktor dari P(x) = x3 + 4x2 + x – 6.
Pembahasan 11
P(x) berderajat 3 sehingga maksimum faktornya berderajat satu yang diperoleh 3 buah. Jika (x – k) merupakan faktor dari P(x) = x3 + 4x2 + x – 6 maka nilai k yang diperoleh yaitu pembagi bundar dari –6, yaitu ±1, ±2, ±3, dan ±6. Nilai-nilai k tersebut disubstitusikan pada P(x).
• Untuk k = –1 → P(–1) = (–1)3 + 4(–1)2 + (–1) – 6 = –4.
P(–1) ≠ 0 maka (x + 1) bukan faktor dari P(x).
• Untuk k = 1 → P(1) = 13 + 4 . 12 + 1 – 6 = 0.
P(1) = 0 maka (x – 1) faktor dari P(x).
• Untuk k = –2 → P(–2) = (–2)3 + 4(–2)2 – 2 – 6 = 0
P(–2) = 0 maka (x + 2) faktor dari P(x).
• Untuk k = 2 → P(2) = 23 + 4 . 22 + 2 – 6 = 20
P(2) ≠ 0 maka (x – 2) bukan faktor dari P(x).
• Untuk k = –3 → P(–3) = (–3)3 + 4(–3)2 – 3 – 6 = 0
P(–3) = 0 maka (x + 3) faktor dari P(x).
• Untuk k = 3 → P(3) = 33 + 4 . 32 + 3 – 6 = 60
P(3) ≠ 0 maka (x – 3) bukan faktor dari P(x).
5.2. Penggunaan Teorema Faktor untuk Mencari Akar Persamaan Suku Banyak
Diketahui, P(x) suku banyak dengan bentuk:
P(x) = anxn + an–1 . xn–1 + … a1x + a0
(x – k) yaitu faktor linear P(x) kalau dan hanya kalau k akar persamaan P(x) = 0. Jika suku banyak P(x) berderajat n maka persamaan P(x) = 0 maksimum memiliki n buah akar.
Contoh Soal 12 :
Tentukan akar-akar bundar untuk suku banyak x2 – 2x – 3 = 0.
Penyelesaian :
Akar bundar untuk x2 – 2x – 3 yaitu pembagi bundar dari –3, yaitu
k = {±1, ±3}.
Suku banyak P(x) = x2 – 2x – 3 berderajat 2 sehingga maksimum banyak akar persamaan yaitu dua. Untuk memperoleh akar-akar tersebut, hitunglah P(k) untuk setiap nilai k. (lihat Teorema 2)
• Untuk k = 1 → P(1) = 12 – 2 . 1 – 3 = –4.
P(1) ≠ 0 sehingga x = 1 bukan akar persamaan suku banyak x2 – 2x – 3 = 0.
• Untuk k = –1 → P(–1) = (–1)2 – 2(–1) – 3 = 0.
P(–1) = 0 sehingga x = –1 akar persamaan suku banyak x2 – 2x – 3 = 0.
• Untuk k = 3 → P(3) = 32 – 2 . 3 – 3 = 0.
P(3) = 0 sehingga x = 3 akar persamaan suku banyak x2 – 2x – 3 = 0.
Anda kini sudah mengetahui Suku Banyak. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.